7.3. Основные следствия системы уравнений Максвелла
В настоящем курсе нет возможности рассмотреть все следствия системы уравнений Максвелла, поэтому ниже ограничимся рассмотрением закона сохранения электрического заряда, закона сохранения электромагнитной энергии (теорема Пойтинга) и обсудим некоторые особенности явления распространения электромагнитных волн.
7.3.1. Закон сохранения электрического заряда.
Закон сохранения электрического заряда неявно содержится в системе уравнений Максвелла. Действительно, вычислим величину дивергенции от правой и левой частей уравнения (7.2)
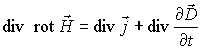 .
В векторном анализе известен результат (его можно проверить непосредственным вычислением!)
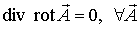 .
Поскольку операция вычисления дивергенции сводится к дифференцированию по пространственным координатам, то порядок вычисления частной производной по времени и вычисления дивергенции можно поменять местами, а если при этом воспользоваться уравнением (7.3), то получим
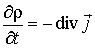 | (7.13) |
- закон сохранения электрического заряда в дифференциальной форме (дивергентная форма). Интегральная форма этого закона имеет вид
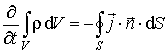 | (7.14) |
или в более привычной форме записи
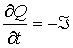 . . | (7.15) |
Физический смысл полученных интегральных соотношений: в фиксированном объеме величина электрического заряда может измениться только при наличии тока (т.е. движения электрических зарядов) через замкнутую поверхность, ограничивающую этот объем. Закон сохранения электрического заряда в дивергентной форме не содержит объемной плотности источников заряда. Отсюда следует, что в классической электродинамике электрический заряд не может возникнуть и не может исчезнуть.
Теорема Пойтинга описывает закономерности изменения во времени энергии электромагнитного поля, связанные с излучением энергии в окружающее пространство, диссипацией (джоулево тепло) и мощностью внешних сил.
Если уравнение (7.1) скалярно умножить на вектор 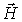 , а уравнение (7.2) скалярно умножить на вектор 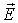 и из первого уравнения вычесть второе, получим:
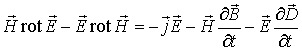 . . | (7.16) |
Непосредственным вычислением можно проверить, что
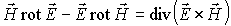 . . | (7.17) |
Если электрические характеристики среды постоянны во времени 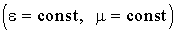 , то
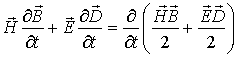 . . | (7.18) |
Используя полученные результаты, приходим к соотношению:
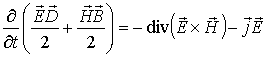 . . | (7.19) |
В левой части соотношения (7.19) стоит частная производная по времени от суммы объемных плотностей энергии электрического поля 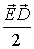 (с этой величиной мы встречались в электростатике) и магнитного поля 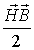 (с этой величиной мы встречались в магнитостатике), а в правой части - типичный для дифференциальных законов сохранения дивергентный член и объемная плотность "источника" электромагнитной энергии. Для сравнения напомним, что уравнение сохранения электрического заряда не содержало объемной плотности источника зарядов.
Векторное произведение 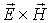 играет роль плотности потока энергии с размерностью Вт/м 2. Его обозначают специальным символом 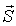 и называют вектором Умова-Пойтинга (в зарубежной литературе - вектор Пойтинга). Заметим, что в уравнении баланса энергии электромагнитного поля вектор Умова-Пойтинга появляется только под знаком дивергенции. Это говорит о том, что физический смысл следует приписать выражению 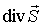 , не вектору 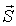 непосредственно. Интерпретация величины потока вектора 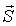 через незамкнутую поверхность всегда требует осторожности.
С использованием уравнения (7.7) источниковый член в соотношении (7.19) можно переписать в форме
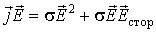 , , | (7.20) |
где первый член правой части - существенно положительная величина, а знак второго члена правой части зависит от взаимной ориентации векторов 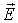 и 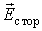 . Первый член представляет собой объемную плотность джоулевых потерь, то есть объемную плотность мощности разогрева среды (Вт/м 3). Второй член - это объемная плотность мощности сторонних сил, с этим членом связана возможность либо получения энергии единицей объема среды, либо совершения работы над окружающей средой.
В интегральной форме соотношение (7.19) имеет вид:
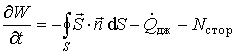 , , | (7.21) |
где 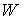 -энергия электромагнитного поля в фиксированном объеме, 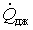 - мощность джоулева тепловыделения, 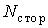 - мощность сторонних сил. Часто о соотношении (7.21) говорят не как о балансовом соотношении, а как о законе сохранения энергии.
7.3.3. Электромагнитные волны.
Система уравнений Максвелла допускает существование переменного электромагнитного поля в пространстве, свободном от электрических зарядов, в форме электромагнитных волн. Уравнения (7.1) и (7.2) для рассматриваемого случая имеют вид:
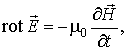 | (7.22) |
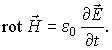 | (7.23) |
Вычислим, например, ротор от обеих частей уравнения (7.22):
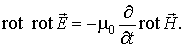 | (7.24) |
Из векторного анализа известно, что
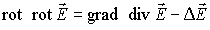 , , | (7.25) |
оператор Лапласа 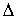 в выражении (7.25) применяется к каждой компоненте векторного поля 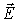 .
Из уравнения (7.3) исходной системы уравнений Максвелла для рассматриваемого случая имеем
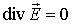 , , | (7.26) |
что с учетом уравнения (7.23) позволяет получить
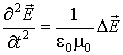 . . | (7.27) |
В одномерном случае из уравнения (7.27) следует
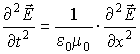 | (7.28) |
(для каждой компоненты вектора 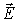 ).
Сравнивая уравнение (7.28) с уравнением
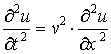 , , | (7.29) |
описывающим распространение бегущей волны с фазовой скоростью 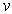 вдоль оси 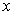 , находим, что
а) каждая из компонент вектора 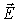 описывается волновым уравнением, т. е. представляет собой волну, бегущую вдоль оси 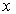 ;
б) фазовая скорость этой волны равна
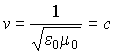 , , | (7.30) |
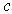 - скорость света (здесь использованы теоретические значения электрической и магнитной постоянных).
Заметим, что можно было бы провести выкладки, вычисляя ротор от обеих частей уравнения (7.23) и исключая поле 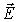 из получающегося уравнения с помощью уравнения (7.22). На этом пути приходят к уравнению
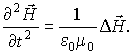 | (7.31) |
Оказывается, что и векторное поле 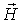 имеет волновой характер, причем фазовая скорость волны 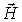 совпадает с фазовой скоростью волны 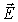 .
Анализ системы уравнений (7.27) и (7.31) на первый взгляд приводит к выводу, что волны 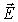 и 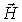 совершенно независимы друг от друга. На самом деле это не так. Если исследовать решения уравнений (7.22) и (7.23) непосредственно, оказывается, что плоские волны 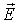 и 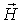 специальным образом ориентированы друг относительно друга, имеют одну и ту же начальную фазу колебаний и согласованные между собой амплитуды. Частоты и волновые векторы у этих волн одинаковы.
Интересно, почему система уравнений (7.27), (7.31) не позволяет все это обнаружить? Дело в том, что система (7.27), (7.31) получена из исходных уравнений (7.22)- (7.23) дифференцированием: исходная система - это система двух дифференциальных уравнений первого порядка, а конечная - система двух уравнений второго порядка. Повышение порядка производных в уравнении расширяет класс допустимых решений. Формально независимые волны 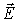 и 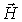 как решения системы (7.27), (7.31) содержат, в частности, и такие, которые являются решениями системы (7.22)- (7.23) с описанными выше свойствами, т. е. реальные электромагнитные волны.
В реальной бегущей электромагнитной волне отличен от нуля средний по времени вектор Умова-Пойтинга
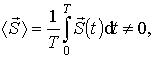 | (7.32) |
что позволяет говорить о том, что бегущая электромагнитная волна переносит энергию. Среднее по времени значение 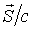 является плотностью потока импульса, а величина 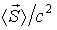 - плотность потока "массы", переносимой электромагнитной волной. Наличие нулевой величины плотности импульса теоретически позволяет рассчитать силу давления, которое оказывает электромагнитная волна на твердую не абсолютно прозрачную поверхность.
В момент создания системы уравнений Максвелла экспериментально электромагнитные волны не были известны. Их несколько позже обнаружил Г.Герц. Тот факт, что свет является совокупностью электромагнитных волн, стало неоспоримым после знаменитых опытов Лебедева по измерению давления света. Теория электродинамики Максвелла стала общепризнанной.
|