4.3. Магнитный диполь во внешнем магнитном поле
Рассмотрим малый тонкий замкнутый контур 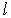 , по которому течет ток  в направлении вектора 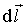 . Если этот контур помещен во внешнее по отношению к нему магнитное поле с магнитной индукцией 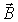 , то по выражению для силы Ампера можно рассчитать силу, действующую на контур в целом:
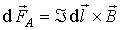 , , | (4.23) |
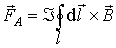 . . | (4.24) |
При вычислении выражения (4.24) оказывается полезной обобщенная теорема Стокса (математическое утверждение):
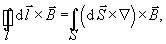 | (4.25) |
где оператор  имеет общепринятое представление. Воспользуемся допущением, что характерный линейный размер контура с током (магнитный диполь) мал по сравнению с характерным линейным размером, на котором существенно изменяются параметры внешнего магнитного поля, и вынесем из под знака интеграла мало меняющиеся величины:
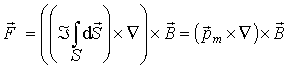 . . | (4.26) |
Далее используем известное тождество векторного анализа
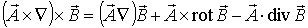 ,
и то обстоятельство, что  , и получим:
 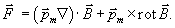 | (4.27) |
Заметим, что формула (4.27) отличается от подобной ей формулы для электрического диполя в электрическом поле напряженности  вторым слагаемым. Дело в том, что в электростатике имеет место уравнение  , а в магнитостатике имеем 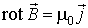 , поэтому в отсутствие объемной плотности токов 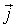 , текущих в точке расположения диполя  , получаем
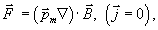 | (4.28) |
а в общем случае справедлива формула (4.27). С учетом того, что величина 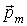 - постоянная векторная величина, а 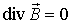 , формулу (4.27) можно записать в виде:
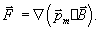 | (4.29) |
Из полученных зависимостей следует, что результирующая сила, действующая на малый контур с током во внешнем магнитном поле, отлична от нуля только в неоднородном векторном поле магнитной индукции 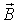 .
| Рис. 4.4.
Магнитный диполь взаимодействует с внешним магнитным полем |
Элементарный момент силы Ампера, действующий на элемент 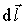 контура с током  , относительно начала координат описывается выражением:
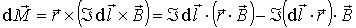 , , | (4.30) |
где 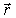 - радиус-вектор расположения элемента  . Для замкнутого контура имеем:
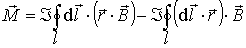 | (4.31) |
После использования обобщенной теорема Стокса получаем:
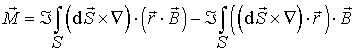 . . | (4.32) |
Вынося за знак интеграла медленно меняющиеся функции и вспоминая определение магнитного момента диполя, получаем:
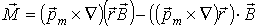 | (4.33) |
Далее используем соотношения:
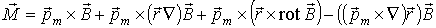 . . | (4.34) |
Последний член в правой части формулы (4.34) тождественно равен нулю, а второй и третий связаны с расстоянием диполя от начала координат. Если начало координат расположить в месте расположения диполя, эти члены обратятся в ноль. Только первое слагаемое формулы (4.34) не зависит от выбора начала координат и в силу этого представляет собой момент сил, действующий на малый замкнутый контур с током во внешнем магнитном поле с магнитной индукцией 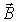 :
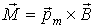 . . | (4.35) |
Выражение (4.35) совпадает по форме с аналогичным выражением для момента сил, действующих на малый электрический диполь  во внешнем электрическом поле напряженности 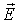 . Момент  обращается в ноль при условии параллельности (или антипараллельности) векторов 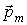 и 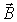 , т. е. если 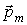 направлен строго по внешнему полю 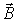 , или строго против внешнего поля  . При малом отклонении вектора 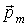 от направления  (если это направление было состоянием равновесия) возникающий момент сил имеет "возвращающий" характер и в гармоническом приближении пропорционален углу отклонения.
Если вернуться к формуле (4.29), то ее структура позволит нам сделать предположение, что потенциальная функция магнитного диполя во внешнем магнитном поле имеет вид.
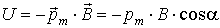 , , | (4.36) |
где  - угол между векторами 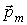 и 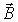 .
Ниже обсудим границы применимости соотношения (4.36). Вычислим дифференциал функции (4.36):
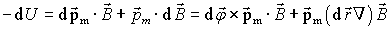 . . | (4.37) |
Изменение потенциальной функции (4.37) учитывает возможность поворота вектора  на угол   и смещение его как целого на вектор  , при этом предполагается, что модуль величины 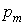 сохраняет постоянное значение. Из соотношения (4.37) можно получить:
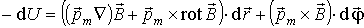 | (4.38) |
В зависимости (4.38) сомножитель при  представляет собой силу, а сомножитель при элементарном угле поворота  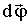 - момент сил, действующих на магнитный диполь.
Благодаря этим результатам выражение (4.36) можно принять за потенциальную функцию магнитного диполя во внешнем магнитном поле.
Заметим, что в соответствии с выражением (4.36) потенциальная функция магнитного диполя во внешнем магнитном поле минимальна, если вектор магнитного момента диполя ориентирован по силовой линии магнитной индукции, и максимальна, если вектор магнитного момента диполя ориентирован строго против направления вектора магнитной индукции. Состояние системы с первой ориентацией более предпочтительное, состояние со второй ориентацией является неустойчивым.
Существенным различием проявления свойств электрического и магнитного диполей является то, что электрический диполь "внутри себя" ослабляет внешнее поле, вдоль силовой линии которого он ориентирован, а магнитный диполь усиливает внешнее поле вдоль силовой линии, если она проходит через "контур диполя". | Рис. 4.5.
Смещение контура с током во внешнем магнитном поле |
Учитывая важность вычисления работы при перемещениях или деформациях замкнутого или разомкнутого контура с током для практических приложений, вычислим эту величину без учета предположения о малой величине замкнутого контура.
Рассмотрим сначала разомкнутый контур с элементом тока 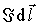 . Если в процессе движения элемент с током смещается на величину 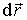 , то работа, совершаемая при этом, равна
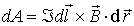 . . | (4.39) |
в силу свойств смешанного произведения векторов, а  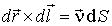 , где 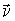 - вектор единичной нормали к элементу поверхности 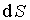 , образованного векторами 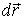 и 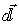 , то из соотношения (4.39) получаем:
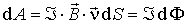 , , | (4.40) |
где 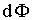 -элемент потока вектора 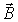 через поверхность 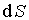 . Для работы в целом имеет место соотношение
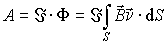 . . | (4.41) |
По выводу зависимости (4.41) поверхность 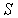 построена как поверхность, "ометаемая" отрезком 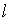 кривой, по которому течет ток, в реальном движении. В силу свойств магнитостатического поля 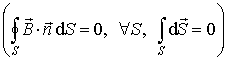 в формуле (4.41) можно использовать любую (произвольную) поверхность, которая опирается на замкнутый контур из начального положения отрезка кривой  , конечного положения отрезка кривой 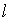 и из траектории начальной граничной точки и траектории конечной граничной точки рассматриваемого отрезка.
Рассмотрим замкнутый контур 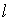 , по которому течет ток  во внешнем магнитном поле с индукцией 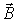 .
| Рис. 4.6.
К расчету работы при перемещении замкнутого контура с током во внешнем магнитном поле |
Пусть начальное положение контура  описывалось кривой 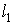 , а конечное -  (рис. 4.3). Пусть на контур 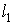 натянута поверхность 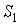 а на контур  натянута поверхность 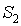 , а боковая поверхность "ометаемого" тела построена как поверхность, по которой перемещается элемент  из положения 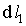 в положение  .
С точностью до бесконечно малых второго порядка запишем выражение для работы по перемещению элемента с током 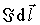 из первого положения во второе:
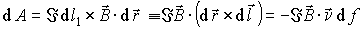 , , | (4.42) |
где  -элемент боковой поверхности описанного выше тела, 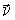 -направление внешней нормали к этому элементу. Из теоремы Гаусса в интегральной форме для вектора  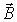 легко получить
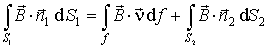 . . | (4.43) |
Из соотношения (4.43) следует:
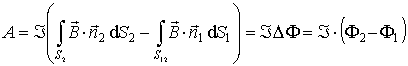 . . | (4.44) |
Соотношение (4.44) получено без использования предположения о малости контура с током.
Для элементарной работы по перемещению контура с током в пространстве получим
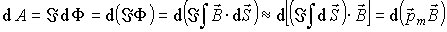 . . | (4.45) |
Подробная последовательность вычислений в формулах (4.45) проясняет, в каком месте существенно использована посылка о малой величине контура с током при выводе соотношения (4.36).
|