2.5. Вектор D. Теорема Гаусса для вектора D в интегральной и дифференциальной формах
В диэлектрической среде могут присутствовать электрические заряды двух типов: "свободные" и "связанные". Первые из них не связаны с молекулярной структурой вещества и, как правило, могут относительно свободно перемещаться в пространстве. Вторые связаны с молекулярной структурой вещества и под действием электрического поля могут смещаться из положения равновесия, как правило, на очень малые расстояния.
Использование напрямую теоремы Гаусса для векторного поля 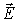 при описании диэлектрической среды неудобно тем, что правая часть формулы
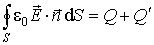 | (2.30) |
содержит как величину "свободного", так и величину "связанного" (некомпенсированного) зарядов внутри замкнутой поверхности 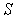 .
Если соотношение (2.30) почленно сложить с соотношением (2.28), получим
 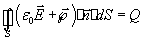 , , | (2.31) |
где 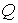 - суммарный "свободный" заряд объема, охватываемого замкнутой поверхность 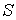 . Соотношение (2.31) обуславливает целесообразность введения специального вектора
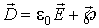 | (2.32) |
в качестве удобной расчетной величины, характеризующей электрическое поле в диэлектрической среде. Вектор 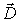 раньше называли вектором электрической индукции или вектором электрического смещения. В настоящее время входит в употребление термин "вектор 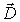 ".
Для векторного поля 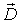 справедлива интегральная форма теоремы Гаусса:
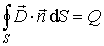 | (2.33) |
и, соответственно, дифференциальная форма теоремы Гаусса:
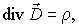 | (2.34) |
где 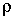 - объемная плотность свободных зарядов.
Если справедливо соотношение (2.27) (для жестких электретов оно не справедливо), то для вектора 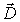 из определения (2.32) следует
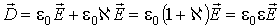 , , | (2.35) |
где 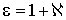 - диэлектрическая проницаемость среды, одна из важнейших электрических характеристик вещества. В электростатике и квазистационарной электродинамике величина 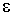 является действительной. При рассмотрении высокочастотных колебательных процессов фаза колебания вектора 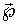 , а значит и вектора 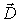 , может не совпадать с фазой колебаний вектора 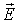 , в таких случаях величина 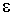 становится комплекснозначной величиной.
Рассмотрим вопрос, при каких условиях в диэлектрической среде возможно появление некомпенсированной объемной плотности связанных зарядов. Для этой цели запишем выражение вектора поляризации 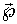 через диэлектрическую проницаемость среды 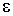 и вектор 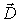 :
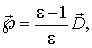 | (2.36) |
в справедливости которого легко убедиться. Теперь представляющая интерес величина 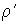 может быть вычислена:
 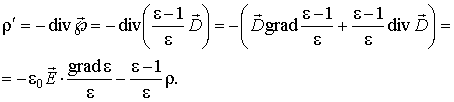 | (2.37) |
 В отсутствие в диэлектрической среде объемной плотности свободных зарядов 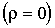 величина 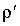 может обратиться в нуль, если
а) отсутствует поле 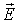 ;
или б) среда однородна  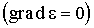
или в) векторы 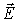 и 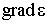 - ортогональны.
 В общем случае необходимо вычислить величину 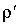 по соотношениям (2.37).
|