7.6. Фазовые переходы второго рада
Описание фазовых переходов второго рода проведем в соответствии с методом, предложенным в 1933 году физиком-теоретиком Паулем Эренфестом (1880 - 1933). Для таких переходов уравнение Клапейрона-Клаузиуса не применимо, так как из условия равенства первых производных удельного термодинамического потенциала
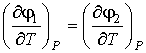 , , | (7.59) |
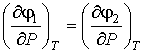 | (7.60) |
в соответствии с формулами (4.52) и (4.53) следует равенство удельных энтропий и объемов
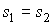 , , | (7.61) |
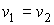 . . | (7.62) |
Это приводит к тому, что в правой части уравнения (7.50) одновременно обращаются в нуль числитель и знаменатель, и в уравнении Клапейрона-Клаузиуса возникает неопределенности вида 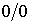 .
Найдем полные дифференциалы удельных энтропий и объемов, и в соответствии с формулами (7.61) и (7.62) приравняем их
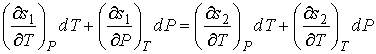 , , | (7.63) |
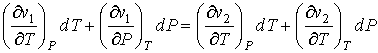 . . | (7.64) |
Проведем преобразование полученных выражений. Производная удельной энтропии по температуре в обратимом процессе может быть представлена в виде
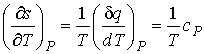 , , | (7.65) |
где: 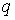 - удельная теплота, 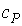 - удельная изобарическая теплоемкость.
Так как для второй производной удельного термодинамического потенциала может быть записано равенство
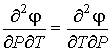 , , | (7.66) |
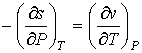 . . | (7.67) |
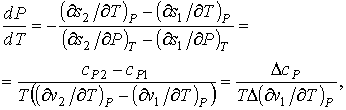 | (7.68) |
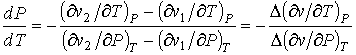 , , | (7.69) |
где символом  обозначена операция нахождения разности соответствующих величин.
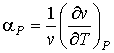 | (7.70) |
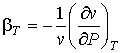 . . | (7.71) |
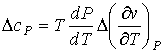 , , | (7.72) |
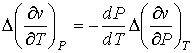 . . | (7.73) |
Наиболее иллюстративным примером фазового перехода второго рода является превращение жидкого Не I в жидкий Не II при температуре 2,2 К и ниже (см. рис. 7.7). С этим фазовым переходом связано квантовое явление сверхтекучести, возникающее в Не II. Это явление было открытое в 1938 г. П.Л. Капицей и теоретически объяснено советским физиком-теоретиком Львом Давыдовичем Ландау (1908 - 1968). Феноменологическая теория сверхтекучести основывается на предложении о том, что Не II представляет собой смесь двух жидкостей, хотя с точки зрения квантовой физики атомы Не II нельзя разделить на два различных вида. Однако классическая аналогия наиболее удобна для восприятия и согласно ей одна компонента Не II является сверхтекучей, а другая - нормальной (не сверхтекучей). Таким образом течение Не II можно представить в виде потоков двух жидкостей, при этом вязкость сверхтекучей компоненты равна нулю.
Именно в отсутствии вязкости у Не II и состоит явление сверхтекучести. Отсутствие вязкости приводит к тому, что Не II может проникать через очень узкие капилляры (П.Л. Капица ставил опыты по протеканию Не II между двумя шлифованными стеклами), а также к тому, что уровни Не II, налитого в два разделенных перегородкой сосуда, постепенно выравниваются из-за образования ползущей пленки (см. рис. 7.12). | Рис. 7.12.
Образование ползущей пленки в сосудах с Не II |
Ползущая пленка имеет толщину менее 10 -7 м. При её движении со скоростью несколько десятков сантиметров в секунду жидкость перетекает из одного сосуда в другой.
Нормальная компонента переносит при своем движении теплоту, а сверхтекучая компонента - нет. При протекании Не II через узкую щель, перетекает главным образом сверхтекучая часть Не II. Поэтому вытекающий Не II должен иметь более низкую температуру, чем Не II в сосуде из которого происходит вытекание. Это явление было использовано для получения сверхнизких температур, составляющих десятые доли кельвина.
К фазовым переходам второго рода относятся также переход некоторых веществ в сверхпроводящее состояние при низких температурах. Такой переход сопровождается падением до нуля электрического сопротивления сверхпроводников.
Примером фазового перехода второго рода является переход железа из ферромагнитного в парамагнитное состояние в точке Кюри. К ним относятся также переходы, связанные с изменением симметрии кристаллической решетки, в тех случаях, когда тип симметрии решетки при переходе становится другим (например, переход от кубической к тетрагональной решетке).
При фазовом переходе второго рода все свойства вещества изменяются непрерывным образом во всем объеме вещества. Поэтому при фазовых переходах второго рода невозможно существование метастабильных состояний, характерных для фазовых переходов первого рода.
|