7.5. Диаграммы состояния
При описании состояния вещества и его фазовых переходов обычно используются переменные 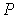 и 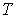 , в которых изображаются кривые равновесия при фазовых переходах данного вещества. Диаграмма, построенная в этих переменных, называется диаграммой состояния. Каждой точке на этой диаграмме соответствует определенное равновесное состояние. Она позволяет определить, какие фазовые переходы происходят при тех или иных процессах.
Рассмотрим случай термодинамической системы, в которой в равновесии находятся сразу три фазы однородного по физико-химическим свойствам вещества (например: лед, вода и пар). Равновесие такой системы будет наблюдаться при одновременном выполнении трех условий, соответствующих равновесию этих фаз между собой. Эти условия в общем виде можно записать в форме
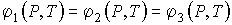 . . | (7.52) |
Равенства (7.52) приводят к системе из двух независимых уравнений
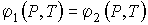 , , | (7.53) |
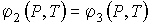 . . | (7.54) |
Решение этой системы уравнений при условии отсутствия химических превращений дает совершенно определенные значения давления 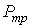 и температуры 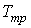 , при которых три фазы могут существовать одновременно. Точка на диаграмме состояния в переменных 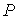 и  (см. рис. 7.6), соответствующая указанным значениям давления и температуры, называется тройной точкой. В этой точке встречаются кривая плавления 1, разделяющая твердую и жидкую фазы, кривая испарения 2, разделяющая жидкую и газообразную фазы, и кривая возгонки 3, разделяющая твердую и газообразную фазы. | Рис. 7.6.
Диаграмма состояния
1 - кривая плавления, 2 - кривая испарения, 3 - кривая возгонки |
Кривая испарения 2 заканчивается критической точкой (К), в которой исчезают отличия жидкой и газообразной фаз. Если фазовый переход осуществляется в обход критической точки, как показано пунктирной линией на рис. 7.6, то пересечения кривой испарения не происходит и фазовое превращение проходит путем непрерывных изменений без образования границы раздела фаз.
Для однородного по своим физико-химическим свойствам вещества в равновесии одновременно могут находиться не более трех фаз. Это означает, что для равновесной системы могут существовать только точки, в которых сходятся три фазы вещества, например, соответствующие трем его агрегатным состояниям. Точки, в которых могли бы одновременно существовать более трех фаз, не реализуемы.
Вещество в трех различных агрегатных состояниях может наблюдаться и при значениях температуры и давления, не соответствующих тройной точке. Например, в природе при различных погодных условиях наблюдаются одновременно лед, вода и водяной пар (последний, как правило, косвенным образом). Однако, в отличие от состояния в тройной точке, указанные состояния не являются равновесными, и для них характерен постоянный переход вещества из одной фазы в другую.
Значения давления и температуры в тройной точке для различных веществ очень стабильны, что позволяет использовать тройную точку для калибровки различных температурных шкал. Тройная точка воды используется в качестве основной реперной точки для температурных шкал Кельвина и Цельсия (см. параграф 1.3).
Отличительной особенностью гелия, диаграмма состояния которого схематически изображена на рис. 7.7, является отсутствие тройной точки, соответствующей одновременному равновесному существованию твердой, жидкой и газообразной фаз. | Рис. 7.7.
Диаграмма состояния гелия
1 - кривая плавления, 2 - кривая испарения, 3 - кривая раздела жидких фаз Не I и Не II, А и В - тройные точки |
Из рис. 7.7 следует, что кривые плавления и испарения у гелия не пересекаются, так как твердая фаза образуется только при давлении свыше 25 атм, а при давлении менее 25 атм гелий остается жидким вплоть до абсолютного нуля температуры (это свойство гелия объясняется с использование квантовой механики). Однако это не означает, что у него нет тройных точек. Дело в том, что гелий имеет две жидкие фазы: Не I и Не II, отличающиеся по своим свойствам. Изображенные на рис. 7.7 точки А и В являются тройными, где сосуществуют в равновесном состоянии три фазы: Не I , Не II и, соответственно, - кристаллический гелий (точка А) или газообразный гелий (точка В). Температура, соответствующая точке В, равна приблизительно 2,2 К.
Как правило, все твердые вещества имеют несколько фазовых состояний, обусловленных различными кристаллическими модификациями, структурно отличающимися между собой. Эти фазы могут точно так же находиться в состоянии равновесия между собой, как и фазы, связанные с различными агрегатными состояниями. На диаграмме состояния условиям равновесия этих фаз соответствуют кривые равновесия при фазовых переходах. Существуют тройные точки, в которых могут одновременно находиться в равновесии три фазы, две из которых представляют собой кристаллические модификации, а одна либо жидкая, либо газообразная. У некоторых веществ тройные точки наблюдаются при равновесии трех различных кристаллических модификаций.
Свойство вещества иметь несколько кристаллических модификаций называется полиморфизмом. Этим свойством, например, обладают сера, углерод, олово и железо. Лед имеет несколько кристаллических модификаций. Фазовый переход из одной кристаллический модификации в другую называется полиморфным превращением, которое в большинстве случаев является фазовым переходом первого рода и сопровождается поглощением или выделением теплоты.
На рис. 7.8 схематически изображены области метастабильных состояний при фазовом переходе жидкость-газ. Выше линии 2 находится область, соответствующая переохлажденному пару, а ниже - перегретой жидкости. Вещество в указанных метастабильных состояниях используется в таких физических приборах как камера Вильсона и пузырьковая камера, принципы работы которых рассматриваются ниже. | Рис. 7.8.
Диаграмма метастабильных состояний при фазовом переходе жидкость-газ
1 - кривая плавления, 2 - кривая испарения, 3 - кривая возгонки |
Если изобразить изотермы двухфазной системы жидкость-газ (см. рис. 7.9), то горизонтальная часть изотерм будет соответствовать фазовому переходу вещества, справа от горизонтальной части лежат изотермы газовой фазы, а слева - жидкой. Пунктирные линии соответствуют метастабильным состояниям. Справа - переохлажденный пар, слева - перегретая жидкость. Эти состояния будут возникать в том случае, если зародыши другой фазы (капли и пузырьки соответственно) отсутствуют или у них имеется тенденция к исчезновению. Так как образованию зародышей способствуют всякого рода примеси и неоднородности, то метастабильные состояния свойственны хорошо очищенным веществам. | Рис. 7.9.
Изотермы двухфазной системы жидкость-газ |
Так как давление переохлажденного пара превышает давление насыщенного пара при той же температуре, то такой пар называется пересыщенным. Образование и рост зародышей жидкой фазы в таком паре будет зависеть от многих факторов и в первую очередь от размеров зародышей, температуры и степени пересыщения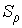 . Степень пересыщения определяется как отношение плотности пересыщенных паров к плотности насыщенных паров
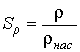 , , | (7.55) |
а при адиабатическом расширении она может быть рассчитана с помощью соотношения
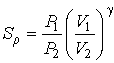 , , | (7.56) |
где:  ,  и 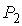 , 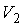 - начальные и конечные давления и объемы пара.
Опыты, проведенные в середине XIX века показали, что если в паре содержатся частицы пыли, то даже при небольшом пересыщении образуется туман и происходит переход из точки А в точку В (см. рис. 7.9). Такой процесс происходит в атмосфере, когда потоки, вызванные конвекцией, поднимают вверх воздух, содержащий водяной пар, где происходит его расширение, сопровождающееся уменьшением температуры. Это приводит к возникновению тумана и росту дождевых капель за счет избыточной концентрации пара по сравнению с насыщенным состоянием.
В 1870 г. Томсоном (лордом Кельвином) было показано, что вследствие поверхностного натяжения давление насыщенного пара  над поверхностью капли, имеющей радиус 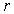 , больше, чем давление пара  над плоской поверхностью жидкости, причем они связаны соотношением (см. задачу 7.5 в конце параграфа)
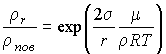 , , | (7.57) |
где: 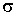 - поверхностное натяжение, 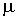 и  - молярная масса и плотность жидкости, 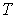 - абсолютная температура, 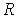 - универсальная газовая постоянная. Отсюда следует, что, если степень пересыщения пара превосходит величину, задаваемую правой частью соотношения (7.57), капли будет расти и образуется туман.
Чем мельче капли, тем большее пересыщение требуется для того, чтобы эти капли не испарялись, а росли. Для воды при 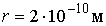 имеем 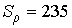 , то есть молекулы, как правило, не могут являться центрами конденсации. Однако эксперимент показывает, что при 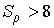 в водяных парах начинает образовываться туман. Английский физик Джозеф Джон Томсон (1856 - 1940) объяснил это тем, что вследствие взаимодействия (коагуляции), молекулы воды образуют капли, наибольший размер которых 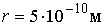 , что соответствует  . При меньших значениях  туман возникает только тогда, когда есть посторонние включения, например, пыль.
Английский физик Чарльз Томсон Рис Вильсон (1869 - 1959) экспериментально показал, что при определенных условиях образование тумана может эффективно происходить на заряженных ионах. На поверхность заряженной капли действуют электростатические силы, изменяющие давление паров вблизи капли, что приводит к изменению условий конденсации. Это обстоятельство позволило Вильсону в 1912 году разработать очень остроумный метод детектирования заряженных частиц ядерного излучения, реализованный в приборе, названном камерой Вильсона.
В этом приборе пересыщенный пар, как правило, состоящий из смеси воды, спиртов и инертных газов, создается адиабатическим расширением с помощью поршня в сосуде с прозрачными стенками. При попадании частицы ионизирующего излучения в сосуд вдоль ее траектории возникает след из ионов, на которых происходит конденсация жидкости и образуется видимый трек, состоящий из капель жидкости. Таким образом, энергия, запасенная в метастабильном состоянии, используется для визуализации ядерных излучений. Зарегистрировать след частицы и его форму можно с помощью фотографирования следа.
Принципиальная схема камеры Вильсона изображена на рис. 7.10. В изолированном рабочем объеме 1 находятся пары воды и спирта в непересыщенном, но близком к насыщению состоянии. Резкое движение диафрагмы 6, которую тянет поршень 4, приводит к быстрому адиабатическому расширению этих паров в объеме 1. При этом достигается степень пересыщения паров, лежащая обычно в пределах от 1,25 до 1, 37. Для ее оценки может быть использовано соотношение (7.56). | Рис. 7.10.
Схема камеры Вильсона
1 - изолированный рабочий объем, 2 - стеклянный цилиндр, 3 - стеклянное окно, через которое производится фотографирование, 4 - подвижный поршень, 5 - регулятор хода поршня, 6 - резиновая диафрагма, 7 - проволочная сетка для уменьшения турбулентности при движении диафрагмы, 8 - впускное отверстие для водно-спиртовой смеси (во время работы оно закрыто), 9 - фотографическое устройство |
При прохождении частиц через объем 1 на их траекториях возникают треки из тумана, которые могут быть сфотографированы. После этого камера Вильсона возвращается в исходное состояние, то есть процесс ее работы является циклическим. Количество циклов достигает обычно от 1 до 6 в минуту. Небольшая скорость работы в какой-то степени является недостатком камеры Вильсона, так как, например, английскому физику Патрику Мейнарду Стюарту Блэкетту (1897 - 1974)пришлось получить около миллиона фотографий следов 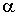 -частиц в азоте, чтобы зафиксировать 20 случаев захвата 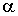 -частицы атомом азота с последующим испусканием протона.
Другим недостатком камеры Вильсона является то, что у нее небольшой объем рабочей камеры (диаметр ее, как правило, составляет несколько десятков сантиметров). Это не позволяет достаточно полно исследовать треки частиц с высокой энергией. Чтобы избежать этого недостатка необходимо использовать более плотное рабочее вещество, в котором длина пробега частиц значительно уменьшается. Поэтому были разработаны пузырьковые камеры, в которых для визуализации треков частиц используется внутренняя энергия, запасенная в перегретой жидкости, высвобождаемая при пролете частицы. Жидкость находится в метастабильном состоянии, описываемом левыми пунктирными линиями на рис. 7.9. При попадании в такую жидкость заряженной частицы вдоль ее траектории образуется след, состоящий из множества пузырьков пара.
Принципиальная схема пузырьковой камеры во многом сходна со схемой камеры Вильсона. Метастабильное состояние (перегретая жидкость) получается, как и в камере Вильсона путем резкого снижения давления. Для того чтобы можно было сфотографировать треки, жидкость должна быть прозрачной. В качестве рабочего тела в пузырьковых камерах используют жидкие водород, пропан и ксенон высокой очистки. Частота циклов пузырьковой камеры достигает десятков в минуту.
Метастабильные состояния системы жидкость-газ наблюдаются в областях параметров, близких к кривой испарения. С повышением температуры плотность насыщенного пара возрастает и при некоторой температуре плотность пара становится равной плотности жидкости. Как в 1860 году установил Менделеев, при достижении этой температуры поверхностное натяжение обращается в нуль. Температура, при которой это происходит, называется температурой абсолютного кипения. При этом исчезает различие между жидкой и газообразной фазами, и кривая испарения заканчивается критической точкой К (см. рис. 7.6 и 7.8). Такое состояние, которое характеризуется определенным набором значений температуры 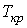 , давления 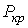 и объема 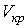 , получило название критического состояния. Для газа Ван-дер-Ваальса значения температуры, давления и объема в критическом состоянии получены в параграфе 2.7.
На рис. 7.11 изображены изотермы системы жидкость-газ, характерные для реальных веществ и подтвержденные многочисленными опытами. Горизонтальный участок этих изотерм, соответствующий одновременному существованию жидкой и газообразной фаз, с ростом температуры уменьшается. Точка, где длина горизонтального участка обращается в нуль и есть критическая точка К, а соответствующая ей температура - критическая температура 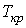 . | Рис. 7.11.
Изотермы системы жидкость-газ, характерные для реальных веществ,
при T1 < T2 < T3 < Tкр < T4 |
При температурах выше критической происходит постепенный переход одной фазы в другую без образования двухфазной системы. Справа от горизонтального участка изотермы пологие, что соответствует большим значениям коэффициента изотермической сжимаемости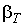 :
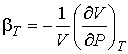 . . | (7.58) |
Это отражает тот факт, что силы межмолекулярного взаимодействия в газе малы, и его молекулы могут перемещаться во всем предоставленном им объеме. Слева от горизонтального участка, наоборот, изотермы идут почти вертикально. Коэффициент изотермической сжимаемости 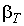 здесь очень мал, что связано с практической не сжимаемостью жидкостей из-за короткодействующих сил межмолекулярного отталкивания. Это явление используется, к примеру, при создании гидравлических прессов.
На горизонтальном участке равенство нулю производной объема по давлению не означает, однако, что коэффициент изотермической сжимаемости становится равным бесконечности. Дело в том, что вышеизложенное относится только к системам с неизменным числом частиц, а при одновременном сосуществовании жидкой и газообразной фаз происходит переход вещества из одной фазы в другую. При изменении давления возникает направленный поток вещества, сопровождающийся изменением объема фаз. Исключение составляет критическая точка К. В ней изотерма имеет точку перегиба, производная давления по объему вблизи точки К стремится к нулю, а коэффициент изотермической сжимаемости 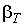 стремится к бесконечности. Это отражает тот факт, что в критическом состоянии вещество представляет собой гомогенную структуру, состоящую из равномерно перемешанных зародышей двух фаз, причем происходит постоянный обмен веществом между зародышами.
Отметим, что для изотерм газа Ван-дер-Ваальса в критической точке К, так же как и для реальных веществ, производная давления по объему обращается в нуль, то есть коэффициент изотермической сжимаемости 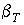 становится равным бесконечности. Описание явлений в критической точки с использованием модели газа Ван-дер-Ваальса проведено в параграфе 7.7.
Переход из жидкого состояния в газообразное (или, наоборот, из газообразного в жидкое) может быть осуществлен по траектории, огибающей критическую точку без пересечения кривой испарения (пунктирная линия на рис. 7.6). В этом случае фазового перехода первого рода с характерным для него скачком первых производных удельного термодинамического потенциала наблюдаться не будет. Переход из жидкого в газообразное состояние будет происходить путем непрерывных изменений без образования границы раздела фаз. При этом среда представляет собой однородную структуру, которая постепенно превращается из жидкости в газ или наоборот. То есть свойства фазы в этом случае меняются непрерывным образом.
При наблюдении перехода в обход критической точки для прозрачного вещества невозможно увидеть никаких резких изменений, так как видимыми могут быть только границы раздела между фазами из-за разности показателей преломления фаз.
Так как в критической точке вещество представляет собой смесь постоянно флуктуирующих зародышей обеих фаз, то в случае наблюдения прозрачного вещества при его прохождении через критическую точку, оно становится мутным. Это позволяет применять оптические методы для исследования свойств веществ в критической точке.
Если переход осуществляется через кривую испарения, то можно наблюдать движение границы раздела жидкость-газ. Будет происходить изменение количества вещества в каждой фазе, при этом свойства фаз остаются неизменными (в случае изотермического перехода).
Непрерывный переход из жидкой фазы в газообразную (или наоборот) возможен потому, что между этими фазами нет принципиальной разницы. Они отличаются только подвижностью молекул (см. параграф 7.1). И в жидкости, и в газах молекулы могут совершать хаотическое поступательное движение.
Однако между твердыми телами и жидкостями существует принципиальная разница. Твердые тела обладают упорядоченной, как правило, анизотропной структурой. В твердом агрегатном состоянии, как указывалось выше, возможны фазовые переходы, обусловленные изменением кристаллической решетки. Вследствие такого принципиального различия не может существовать непрерывного перехода из жидкого в твердое состояние, и, поэтому, критической точки для кривой плавления не существует.
При переходе жидкости в твердое состояние может наблюдаться метастабильное состояние - переохлажденная жидкость. В таком состоянии в частности может находиться вода, охлажденная до температуры ниже 0 оС. Если в таком состоянии в воде возникают зародыше твердой фазы, например, вследствие резкого изменения внешнего давления (при ударе по сосуду, в котором находится переохлажденная вода), то наблюдается очень быстрое превращение воды в лед.
Кривая возгонки стремится к точке с нулевыми значениями давления и температуры (начало координат диаграммы состояния). Это означает, что вещества отвердевают при стремлении к абсолютному нулю температуры. В качестве исключения можно привести гелий, у которого твердое состояние реализуется только при достаточно большом внешнем давлении (см. рис. 7.7).
Задача 7.5. Определить отношение давления насыщенного пара 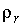 над поверхностью капли, имеющей радиус над поверхностью капли, имеющей радиус 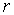 , к давлению пара , к давлению пара  над плоской поверхностью жидкости. над плоской поверхностью жидкости.
Решение: В соответствии с распределением Больцмана (см. формулу (5.23)), концентрация насыщенного пара над поверхностью капли 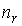 и над плоской поверхностью жидкости и над плоской поверхностью жидкости  связаны соотношением связаны соотношением
 ,
где 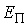 - потенциальная энергия молекулы жидкости на поверхности капли относительно энергии молекулы на плоской поверхности жидкости. Величина - потенциальная энергия молекулы жидкости на поверхности капли относительно энергии молекулы на плоской поверхности жидкости. Величина 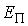 численно равна работе численно равна работе 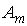 , которую совершают силы поверхностного натяжения при удаления одной молекулы из капли жидкости: , которую совершают силы поверхностного натяжения при удаления одной молекулы из капли жидкости:
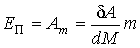 ,
где: 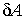 - работа сил поверхностного натяжения при изменении массы капли на величину - работа сил поверхностного натяжения при изменении массы капли на величину 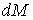 , , 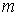 - масса одной молекулы жидкости. - масса одной молекулы жидкости.
Если радиус капли уменьшается при испарении на величину 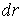 , то её масса уменьшается на величину , то её масса уменьшается на величину
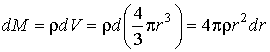 ,
а совершаемая при этом работа равна (см. формулу (7.11))
 ,
где:  - плотность жидкости, - плотность жидкости, 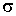 - поверхностное натяжение. - поверхностное натяжение.
Подстановка этих формул в выражение для потенциальной энергии 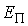 дает дает
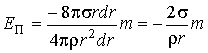 .
Учитывая, что  , где , где 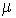 - молярная масса жидкости, имеем - молярная масса жидкости, имеем
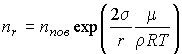 .
Домножение этого выражения на массу одной молекулы (так как плотность равна произведению массы одной молекулы на концентрацию:  ) и деление его на ) и деление его на  дает дает
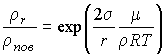 .
Полученное выражение совпадает с формулой (7.57).
|