7.4. Фазовые переходы первого рода
Для описания фазового перехода первого рода необходимо определить зависимость давления от температуры в точках фазового перехода: 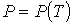 , то есть форму кривой равновесия двух фаз. Применение методов равновесной термодинамики позволяет определить первую производную этой зависимости, или наклон кривой равновесия.
Предположим, что при подводе к одной из фаз двухфазной среды некоторого количества теплоты 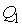 , происходит переход части вещества, массой 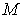 , из первой фазы во вторую. Так как рассматриваемый переход считается квазиравновесным, то давление и температура при его осуществлении постоянны: 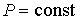 и 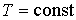 . Удельный объем, определяемый как отношение объема фазы к её массе для первой фазы равен 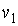 , а для второе - соответственно  . Количество вещества массой 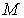 занимает в первой фазе объем  , а во второй - объем 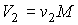 .
Переход вещества из первой фазы во вторую изображен на рис. 7.5 как участок 1-2 некоторого кругового процесса, с помощью которого количество вещества массой  возвращается в исходное состояние в первой фазе. Будем считать, что этот круговой процесс представляет собой цикл Карно. Тогда процессы 2-3 и 4-1 являются адиабатическими, а изотермический процесс 3-4 описывает теплоотдачу при переходе вещества из второй фазы в первую. Считаем, что процесс 3-4 осуществляется при давлении  и температуре 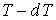 , значения которых бесконечно близки к значениям давления  и температуры 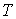 протекания процесса 1-2. | Рис. 7.5.
Диаграмма к расчету фазового перехода первого рода |
На основании первой теоремы Карно (см. параграф 3.5) можно записать выражение для к.п.д. рассматриваемого цикла
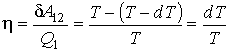 , , | (7.43) |
где 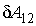 - совершаемая за цикл работа. С учетом бесконечной малости величины 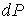 в первом приближении можно считать, что работа  , совершаемая за цикл Карно близка к работе цикла, представляющего собой прямоугольник бесконечно малой высоты. Это позволяет заменить адиабаты на боковых сторонах цикла Карно вертикальными отрезками при 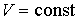 , то есть представить цикл Карно в виде прямоугольника, высота которого равна бесконечно малой величине 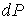 . В этом приближении имеем
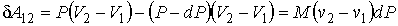 . . | (7.44) |
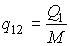 . . | (7.45) |
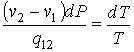 | (7.46) |
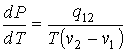 . . | (7.47) |
Это выражение называется уравнением Клапейрона-Клаузиуса. Оно позволяет определить производную давления от температуры при равновесном фазовом переходе первого рода в зависимости от удельной теплоты перехода, его температуры и удельных объемов начальной и конечной фаз.
Уравнение Клапейрона-Клаузиуса можно получить также с помощью удельного термодинамического потенциала. Для этого вычислим полные дифференциалы от правой и левой частей выражения (7.4)
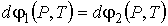 | (7.48) |
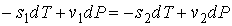 , , | (7.49) |
где:  и  - удельные энтропии первой и второй фаз соответственно.
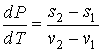 . . | (7.50) |
Так как процесс перехода вещества из одной фазы в другую считается равновесным и происходящим при постоянной температуре, то разность удельных энтропий этих фаз можно определить следующим образом
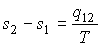 . . | (7.51) |
Подстановка этого выражения в формулу (7.50) приводит её к виду уравнения Клапейрона-Клаузиуса (7.47).
В соответствии с уравнением Клапейрона-Клаузиуса знак производной  зависит от соотношения удельных объем фаз. Если при подводе теплоты жидкость переходит в газообразное состояние, что сопровождается увеличением удельного объема: 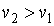 , то производная  . Поэтому при таком переходе повышение давления приводит к увеличению температуры кипения. Аналогичная зависимость наблюдается и при плавлении большинства твердых тел. Исключение составляют вещества, для которых плавление сопровождается уменьшением их удельного объема: 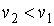 . Примером такого вещества является вода, которая при переходе из замерзшего состояния в жидкое уменьшает свой удельный объем (плотность воды больше плотности льда). Для таких веществ характерно понижение температуры плавления при повышении давления.
Решение: Используя уравнение Клапейрона-Клаузиуса
и считая удельные объемы и теплоту фазового перехода постоянным величинами, получим
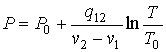 ,
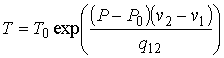 ,
где: 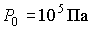 , , 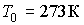 . .
Из полученных формул следует
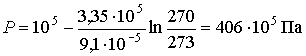 ,
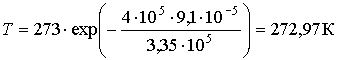 .
Таким образом для расплавления льда при температуре незначительно меньшей нуля градусов Цельсия необходимо создать достаточно большое давление (в рассматриваемом случае порядка 400 атм). Лед под коньком конькобежца плавится за счет его нагревания из-за трения.
Задача 7.4. Определить давление, при котором вода будет кипеть при температуре 90 0С. На какой высоте можно ожидать кипение воды при этой температуре? Считать, что удельный объем пара много больше удельного объема воды: 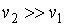 . Удельная теплота испарения воды . Удельная теплота испарения воды  . .
Решение: Будем считать, что к водяному пару применимо уравнение Клапейрона-Менделеева, и он описывается моделью идеального газа. Тогда для удельного объема пара можно записать:
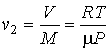 .
С учетом малости удельного объема воды по сравнению с удельным объемом пара, уравнение Клапейрона-Клаузиуса дает
 .
Интегрирование этого уравнения позволяет получить зависимость давления от температуры
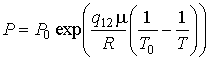 ,
где: 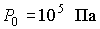 , , 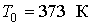 - давление и температура кипения воды при нормальных условиях. - давление и температура кипения воды при нормальных условиях.
Подстановка в это выражения температуры 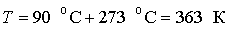 , дает , дает
 .
Таким образом, температура кипения воды уменьшается при уменьшении давления. С этим связан эффект кипения воды в горах при более низкой температуре, чем на уровне моря.
В соответствие с барометрической формулой
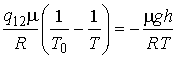 .
 .
Отметим, что при таком перепаде высот барометрическая формула дает только приближенную оценку давления, так как температура атмосферы с подъемом достаточно сильно понижается, и её нельзя считать постоянной.
|