7.2. Условия равновесия фаз
Если среда однородна во всех своих точках, то такая термодинамическая система будет однофазной, а если система состоит из двух (или более) граничащих между собой однородных сред, то это двухфазная (или многофазная) термодинамическая система.
Примером двухфазной системы может служить стеклянный сосуд с налитой в него водой. В этом случае в системе имеется жидкая фаза (вода) и твердая фаза (стекло). Если в состав системы включить окружающий сосуд воздух, то система станет трехфазной. Третья фаза при этом будет газообразной (воздух). Отметим, что смесь газов является однофазной системой, так как в этом случае нет границы раздела.
Находящиеся в равновесии термодинамические системы не обязательно должны представлять собой однородную среду, то есть быть однофазными. В состоянии равновесия может находиться система, состоящая из нескольких различных по своим физико-химическим свойствам фаз, пространственно разделенных не изменяющимися с течением времени (или для квазиравновесного случая бесконечно медленно изменяющимися) границами раздела фаз. Если через эти границы не происходит макроскопический перенос, а сами фазы находятся в состоянии термодинамического равновесия, то такая термодинамическая система, несмотря на свою неоднородность, будет находиться в состоянии термодинамического равновесия.
Для равновесия фаз необходимо, чтобы между ними наблюдалось тепловое и механическое равновесие. Первое из этих условий означает равенство температур  и 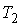 с разных сторон границы раздела фаз: 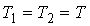 . Второе условие не обязательно соответствует равенству давлений 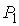 и  с разных сторон границы раздела, так как сама эта граница, в случае, если её форма не представляет собой плоскости, может создавать дополнительное межфазное давление 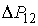 . Поэтому в общем случае условие механического равновесия имеет вид:
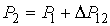 , , | (7.1) |
где: 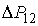 - дополнительное давление на первую фазу, создаваемое границей её раздела со второй. Если считать границы раздела фаз плоскими, то условие (7.1) станет эквивалентным предположению о равенстве давлений по обе стороны границы раздела фаз:  .
В качестве многофазной системы может выступать система, состоящая из фаз одного и тоже вещества, находящегося в различных агрегатных состояниях. Примером такой ситуации может служить система, состоящая из воды, в которой плавает кусочек льда. В состоянии равновесия количество воды и льда в системе неизменно. Но если к такой системе подвести теплоту, то начнется процесс таяния льда, который приведет к изменению границы раздела различных агрегатных состояний, то есть к движению границ раздела фаз. При этом будет происходить процесс превращения вещества из одного агрегатного состояния в другое, то есть фазовое превращение.
Необходимо отметить, что как в случае равновесия различных фаз, так и при фазовых превращениях, процессы на границе раздела носят статистический характер. На границе раздела воды и пара происходит постоянный процесс перехода молекул из воды в пар и обратно. В равновесном состоянии эти встречные процессы взаимно компенсируют друг друга, а при подводе или отводе теплоты один из этих процессов (переход молекул из воды в пар или наоборот) начинает преобладать и это приводит к изменению количества вещества в различных агрегатных состояниях.
Для устойчивого равновесия по отношению к тепловым и механическим воздействиям системы, состоящей из находящихся в различных агрегатных состояниях фаз одного и того же вещества, необходимо потребовать отсутствия макроскопического переноса молекул этого вещества из одной фазы в другую. Возникновение потоков вещества через границу раздела фаз возможно при наличии различных значений удельного термодинамического потенциала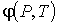 (или химического потенциала  (см. параграф 4.2)) с разных сторон относительно этой границы.
Состояние термодинамического равновесия системы, состоящей из двух находящихся при одинаковых значениях давления 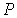 и температуры  фаз, каждая из которых имеет соответственно массы  и 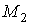 , характеризуется минимумом термодинамического потенциала
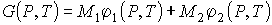 , , | (7.2) |
где:  и 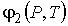 - удельные термодинамические потенциалы первой и второй фаз соответственно. Термодинамический потенциал  является потенциалом Гиббса (см. формулу (4.49)).
Так как при фазовых переходах общая масса вещества  остается неизменной, а происходит только переход частиц из одной фазы в другую, то условие минимума термодинамического потенциала эквивалентно условию его неизменности при изменении массы фаз. Если масса первой фазы уменьшается на величину  , то одновременно возрастает масса второй фазы на эту же величину 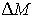 . Тогда термодинамический потенциал 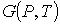 в соответствии с формулой (7.2) становится равным:
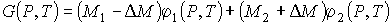 . . | (7.3) |
Если удельный термодинамический потенциал 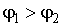 , то минимума функция (7.3) достигает при равенстве нулю массы первой фазы, а при 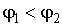 - соответственно в случае равенства нулю массы второй фазы. В обоих этих случаях система переходит в однофазное состояние и условие равновесия двух фаз нарушается.
Таким образом, в дополнение к указанным выше условиям равенства в соприкасающихся фазах температуры  и давления 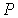 , для обеспечения устойчивого равновесия двух фаз необходимо потребовать равенства их удельных термодинамических потенциалов:
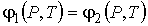 . . | (7.4) |
Отметим, что аналогичное условие должно выполняться и для квазистатических фазовых превращений, для которых различие между удельными термодинамическими потенциалами фаз считается бесконечно малым.
Уравнение (7.4) может быть разрешено относительно переменной 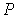 и представлено в виде:
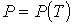 . . | (7.5) |
В отличие от удельных термодинамических потенциалов, величины которых на границе раздела фаз одинаковые, при фазовых превращениях производные этих потенциалов в различных фазах могут быть различными. Если первые производные удельных термодинамических потенциалов для различных фаз не равны между собой:
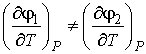 , , | (7.6) |
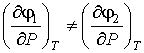 , , | (7.7) |
то такое фазовое превращение называется фазовым переходом первого рода. Характерной особенностью фазовых переходов первого рода является поглощение или выделение теплоты при их осуществлении. К фазовым переходам первого рода относятся превращения при испарении, конденсации, плавлении и кристаллизации вещества.
Если при фазовом превращении первые производные удельных термодинамических потенциалов 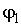 и 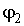 для различных фаз одинаковы, а вторые производные различны, то такие превращения называются фазовыми переходами второго рода. При таких переходах теплота не выделяется и не поглощается, но для них характерны скачкообразные изменения теплоемкости, температурного коэффициента расширения и сжимаемости вещества. Примерами фазовых переходов второго рода являются превращение магнитного сплава из ферромагнитного состояния в парамагнитное, переход металла или сплава в сверхпроводящее состояние и переход жидкого гелия в сверхтекучее состояние.
|