6.4. Броуновское движение
Броуновское движение впервые было экспериментально открыто и исследовано в 1827 году английским ботаником Робертом Броуном (1773 - 1858), который наблюдал в микроскоп взвешенную в воде цветочную пыльцу. Частички этой пыльцы совершали случайные перемещения, причем средняя величина этих перемещений за одинаковые промежутки времени не изменялись при неизменных параметрах жидкости, например, её температуры. При повышении температуры наблюдалось увеличение интенсивности броуновского движения.
Для описания броуновского движения частицы в жидкости предположим, что на неё со стороны частиц жидкость действует случайная сила 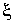 , среднее значение которой равно нулю: 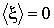 . Тогда можно записать уравнение движения броуновской частицы в направлении выбранной оси 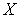 в виде
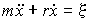 , , | (6.37) |
где: 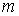 - масса броуновской частицы, 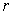 - коэффициент вязкого трения броуновской частицы в жидкости. Умножим правую и левую часть уравнения (6.37) на величину 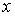 и воспользуемся равенством:
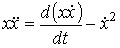 . . | (6.38) |
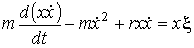 . . | (6.39) |
Проведем усреднение получившегося уравнения по большому количеству броуновских частиц:
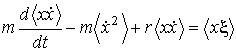 . . | (6.40) |
Вследствие хаотичности движения броуновской частицы можно считать, что величины координаты 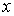 и силы 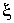 являются взаимно статистически независимыми и среднее значение их произведения равно нулю: 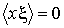 . Кроме того, на основании формулы (5.53) можно записать:
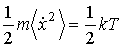 . . | (6.41) |
Тогда уравнение (6.40) принимает вид
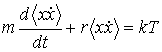 . . | (6.42) |
Будем считать, что в момент времени 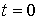 броуновская частица находится в положении с координатой 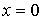 и поэтому 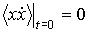 . Для этого случая решение уравнения (6.42) можно записать в форме:
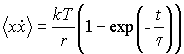 , , | (6.43) |
где постоянная времени 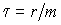 является очень небольшой величиной по сравнению со временем наблюдения броуновской частицы. При 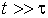 , что соответствует случаю установившегося броуновского движения, имеем
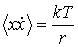 . . | (6.44) |
Воспользовавшись равенством:
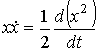 , , | (6.45) |
преобразуем формулу (6.44) к виду:
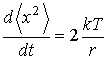 . . | (6.46) |
Интегрирование этого выражения с учетом начального условия 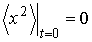 , дает
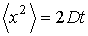 , , | (6.47) |
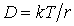 . . | (6.48) |
Формула (6.47) была впервые получена в 1905 году Альбертом Эйнштейном (1879 - 1955) и носит его имя. Независимо от Эйнштейна в 1905 - 1906 годах теория броуновского движения были разработана польском физиком Марианом Смолуховским (1872 - 1917). Полученное им выражение совпадало с формулой (6.47) с точностью до постоянного множителя порядка единицы.
Таким образом, из формулы (6.47) следует, что квадрат перемещения броуновской частицы пропорционален времени, прошедшему с начала наблюдения за ней. В соответствии с формулой (6.48) величина квадрата перемещения броуновской частицы за одинаковые промежутки времени увеличивается с повышением температуры 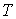 и уменьшается с возрастанием коэффициента вязкого трения 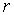 .
Полученные выше формулы были экспериментально проверены в 1908 году Перреном, который измерял с помощью микроскопа перемещения броуновских частиц за одинаковые промежутки времени. Ему удалось на основании своих опытов с помощью формул (6.47) и (6.48) определить постоянную Больцмана 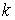 и вычислить значение постоянной Авогадро 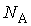 , совпадающие по величине с их значениями, полученными другими методами.
Теория броуновского движения нашла широкое применение не только для описания случайного движения частицы в жидкости, но и для решения целого ряда прикладных задач. Этой теории подчиняются случайные тепловые колебания высокоточных механических и электрических измерительных устройств, таких, например, как крутильные весы и гальванометры. Кинетические уравнения, полученные в теории броуновского движения, используются для анализа точности работы различных систем управления. Они позволяют рассчитать случайные ошибки, возникающие при управлении техническими устройствами и провести оптимизацию их параметров.
Задача 6.2. Определить зависимость от времени среднего квадрата случайных изменений координаты находящейся в вязкой жидкости частицы массой 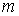 , закрепленной на пружине жесткостью , закрепленной на пружине жесткостью 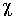 . Коэффициент вязкого трения частицы в жидкости считать равным величине . Коэффициент вязкого трения частицы в жидкости считать равным величине 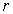 . В начальный момент времени частица находится в положении с координатой . В начальный момент времени частица находится в положении с координатой 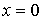 . .
Решение: Запишем уравнение движения частицы в рассматриваемом случае
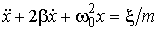 ,
где: 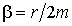 - коэффициент затухания, - коэффициент затухания, 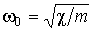 - собственная частота колебаний частицы, - собственная частота колебаний частицы, 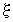 - случайная сила, среднее значение которой равно нулю: - случайная сила, среднее значение которой равно нулю: 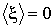 . .
Умножим полученное уравнение на величину 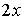 и, воспользовавшись равенствами (6.38) и (6.45), получим и, воспользовавшись равенствами (6.38) и (6.45), получим
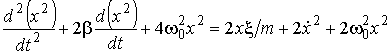 .
Если учесть выражение для средней энергии случайных колебаний осциллятора (см. задачу 5.4):
и провести усреднения, то рассматриваемое дифференциальное уравнение приобретет вид
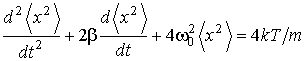 .
Далее для определенности будем считать, что 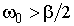 . Тогда с учетом начального условия . Тогда с учетом начального условия 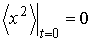 решение этого уравнения можно записать в форме: решение этого уравнения можно записать в форме:
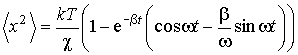 ,
где 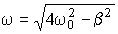 . .
При 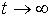 величина квадрата средних флуктуаций координаты частицы величина квадрата средних флуктуаций координаты частицы 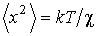 , что соответствует выражению, полученному в задаче 5.4. , что соответствует выражению, полученному в задаче 5.4.
|