6.2. Описание явлений переноса в газах
Процессы переноса в газах могут быть описаны с использованием молекулярно-кинетической теории. Такое описание дает правильные выражения для уравнений переноса и приближенные (с точность до постоянного множителя порядка единицы) формулы для расчета коэффициентов переноса. Полученные значения для коэффициентов переноса оказываются несколько заниженными по сравнению с их выражениями, получаемыми при точных расчетах, которые обычно проводятся с использованием методов статистической физики.
Будем считать, что молекулы газа совершают хаотическое тепловое движение. В этом случае можно предположить, что вероятность движения молекулы в любом направлении одинакова. Так как таких возможных направлений движения всего шесть, соответствующих движению в положительном и отрицательном направлении вдоль осей 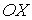 ,  и 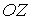 , то плотность потока частиц 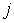 в любом из этих направлений может быть определена по формуле:
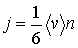 , , | (6.6) |
где:  - средняя скорость теплового движения молекул, 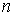 - концентрация молекул газа.
На рис. 6.1 схематически изображен процесс переноса некоторой физической величины 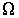 через площадку  . Будем считать, что величина  изменяется в зависимости от координаты 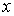 . В качестве переносимой величины может выступать масса, энергия, импульс и т.д. При этом считаем, что переносимую величину можно отнести к одной молекуле. Если речь идет, например, о переносе энергии, то отнесенной к одной молекуле величиной будет полная энергия молекулы. | Рис. 6.1.
Схема к выводу уравнения переноса |
Через площадку 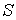 в направлении оси 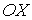 будет проходить поток молекул  , а в противоположном направлении соответственно поток 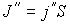 . В случае выполнения принципа детального равновесия, плотности потоков молекул в двух противоположных направлениях должны быть одинаковыми: 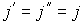 или 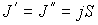 . Переносимый в направлении оси  поток величины  отличается от потока этой величины, переносимого в обратном направлении. Это связано с тем, что в рассматриваемом газе через площадку  в направлении оси  будут проходить молекулы, характеризуемые величиной 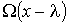 , а в противоположном - соответственно величиной 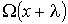 , где 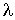 - длина свободного пробега молекул газа, численно равная перемещению, которое молекула газа проходит без соударения с другими молекулами. Тогда плотность потока величины 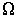 с учетом выражения (6.6) можно вычислить по формуле:
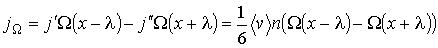 . . | (6.7) |
Считая длину свободного пробега 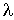 малой величиной, функцию 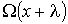 (и соответственно функцию 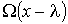 ) можно разложить в ряд с сохранением только слагаемого первого порядка малости:
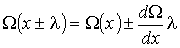 . . | (6.8) |
Тогда разность значений 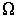 в формуле (6.7) принимает вид:
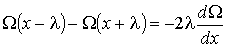 . . | (6.9) |
Окончательно получаем уравнение переноса для плотности потока физической величины  :
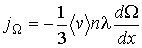 , , | (6.10) |
а соответственно для потока 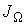 имеем:
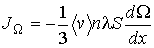 . . | (6.11) |
Стоящие в полученных выражениях (6.10) и (6.11) величины средней скорости 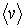 , концентрации молекул 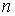 и переносимой физической величины  зависят только от координаты 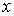 и принимают значения, соответствующие точке с координатой 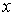 .
Полученное уравнение переноса применимо для описания явлений диффузии, теплопроводности и вязкости в газах при отсутствии в них макроскопического перемешивания.
Проведем описание диффузии примеси одного газа в другом. Для простоты будем считать, что оба газа имеют практически одинаковые молекулы и их суммарная концентрация постоянна и равна величине 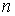 : 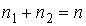 , где 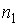 и  - концентрации газов. Введение последнего условия необходимо для того, чтобы в системе не возникало макроскопическое перемешивание газов, а их взаимное проникновение происходило только за счет диффузии.
Пусть концентрация диффундирующего газа  зависит только от одной координаты  : 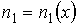 . Тогда физической величиной, перенос которой в данном случае осуществляется вследствие диффузии, является относительная концентрация газа, которая также зависит только от переменной  :
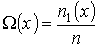 . . | (6.12) |
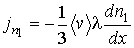 . . | (6.13) |
Соответственно выражение для потока частиц 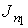 принимает форму:
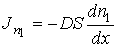 , , | (6.14) |
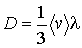 . . | (6.15) |
Выражения, аналогичные формулам (6.13) и (6.14), могут быть записаны и для второго газа, имеющего концентрацию 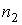 .
Уравнение (6.15) позволяет также записать формулу, описывающую поток массы. Считая, что молекула газа имеет массу  , умножим на эту величину уравнение (6.15) и учтем связь величины потока массы  и потока концентрации частиц 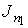 : 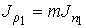 . Тогда имеем:
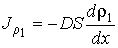 , , | (6.16) |
где: 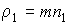 - плотность диффундирующего газа.
С учетом формулы для длины свободного пробега (2.52):
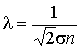 , , | (6.17) |
где 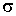 - эффективное сечение молекулы газа, и выражения (5.71) для средней скорости:
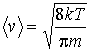 , , | (6.18) |
выражение для коэффициента диффузии приобретает вид:
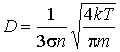 . . | (6.19) |
Как следует из этой формулы, коэффициент диффузии растет с повышением температуры: 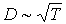 и уменьшается при увеличении концентрации: 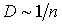 . Уменьшение коэффициента диффузии при увеличении концентрации молекул связано с уменьшением длины свободного пробега 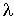 , что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
При описании теплопроводности в качестве переносимой величины 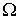 выступает энергия теплового движения молекулы газа:
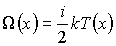 , , | (6.20) |
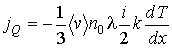 . . | (6.21) |
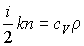 , , | (6.22) |
где: 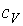 - удельная теплоемкость газа при постоянном объеме, 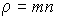 - плотность газа, то уравнение (6.21) приобретет форму
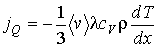 , , | (6.23) |
а выражение для потока теплоты 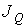 через площадку площадью  , перпендикулярную оси 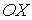 , соответственно запишется в виде:
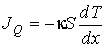 . . | (6.24) |
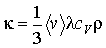 . . | (6.25) |
При подстановке в эту формулу выражений для длины свободного пробега (6.17) и средней скорости (6.18) имеем:
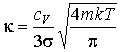 . . | (6.26) |
Из этой формулы следует, что с повышением температуры, коэффициент теплопроводности тоже увеличивается:  . Но в отличие от коэффициента диффузии, этот коэффициент не зависит от концентрации молекул газа.
Эта особенность связана с тем, что в более плотном газе в теплопроводности участвует большее количество молекул. Но при этом, вследствие меньшей длины свободного пробега 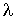 , энергия передается на меньшие расстояния. Для более разреженного газа ситуация обратная: в переносе энергии участвует меньшее число молекул, но этот перенос осуществляется на большие расстояния.
Отметим так же, что независимость теплопроводности от концентрации молекул газа справедлива только в том случае, если в нем отсутствует макроскопическое перемешивание, и перенос энергии осуществляется без переноса вещества.
Явление вязкости газа может быть описано с помощью уравнения (6.10) при подстановке в него в качестве переносимой величины 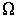 импульса молекулы при упорядоченном движении газа в направлении, перпендикулярном оси  :
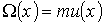 , , | (6.27) |
где: 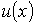 - скорость течения газа в направлении, перпендикулярном оси 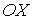 , в точке с координатой  : 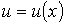 . С учетом формулы (6.27) получим уравнение вязкости в виде:
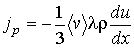 . . | (6.28) |
Тогда формула для расчета потока импульса  приобретет вид
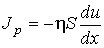 , , | (6.29) |
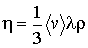 . . | (6.30) |
Величина 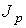 имеет смысл силы, с которой слои газа, двигающиеся в направлении, перпендикулярном оси 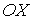 , действуют друг на друга.
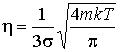 . . | (6.31) |
Температурная зависимость коэффициента вязкости аналогична зависимости для коэффициента теплопроводности: 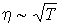 , и этот коэффициент, также как и теплопроводность, не зависит от концентрации молекул газа (плотности газа).
Независимость коэффициента вязкости от плотности газа имеет то же объяснение, что и для теплопроводности. С повышением плотности увеличивается число молекул, переносящих импульс, но уменьшаются расстояния, на которые этот перенос осуществляется.
Как было отмечено выше, коэффициенты диффузии  , теплопроводности  и вязкости  возрастают с увеличением температуры, пропорционально  . Указанная зависимость связана с возрастанием пропорционально  средней скорости движения молекул газа (см. формулу (6.18)). Но, как показывают экспериментальные исследования, эти коэффициенты с повышением температуры растут несколько быстрее, чем 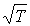 . Это связано с тем, что с увеличением температуры происходит некоторое уменьшение эффективного сечения молекул газа 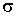 , а величина 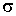 стоит в знаменателях формул для коэффициентов диффузии (6.19), теплопроводности (6.26) и вязкости (6.31).
Между всеми полученными коэффициентами переноса существует общее соотношение, имеющее следующий вид:
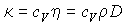 , , | (6.32) |
которое позволяет по результатам измерений одного из коэффициентов переноса вычислять все остальные.
Кроме этого, полученные соотношения дают возможность по экспериментально измеренным коэффициентам диффузии, теплопроводности или вязкости определять длину свободного пробега молекулы газа и её эффективное сечение. Это, в свою очередь, позволяет находить диаметр молекулы.
В заключение отметим еще раз, что полученные выражения для коэффициентов переноса являются приближенными с точностью до некоторого безразмерного множителя порядка единицы.
Задача 6.1. Определить зависимость от температуры коэффициентов диффузии, теплопроводности и вязкости для газа, находящегося при постоянном давлении.
Решение: Будем считать, что уравнение состояния газа имеет вид:
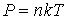 .
Тогда выразив из этой формулы концентрацию газа 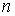 и подставив в выражение (6.19), получим формулу для коэффициента диффузии: и подставив в выражение (6.19), получим формулу для коэффициента диффузии:
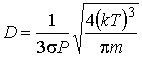 .
Как следует из этой формулы, при указанном процессе коэффициент диффузии пропорционален температуре в степени 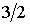 : : 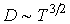 . .
Так как коэффициенты теплопроводности и вязкости не зависят от концентрации молекул газа, и, следовательно, от изменения его давления, то для определения их температурной зависимости можно использовать формулы (6.26) и (6.31) соответственно.
|