5.3. Принцип детального равновесия
Статистическое описание равновесных состояний может быть выполнено с использованием предположения о том, что в равновесной термодинамической системе два любых противоположно направленных процесса должны компенсировать друг друга. Если указанное предположение не выполняется, то это приведет к возникновению в системе упорядоченных движений или процессов, и ее состояние станет неравновесным.
В равновесной термодинамической системе вероятности протекания прямого и обратного процессов одинаковы.
Данная формулировка справедлива для любых, в том числе и микроскопических процессов, имеющих очень малые пространственный размеры. Под обратным процессом понимается такой процесс, который полностью совпадает с прямым при замене течения времени на противоположное. Например, если прямой процесс заключается в соударении двух шаров, при котором их начальные скорости 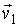 и 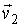 переходят в 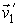 и 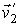 , то при обратном процессе произойдет обратный переход скоростей 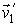 и 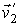 в 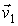 и 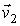 .
Рассмотрим применение принципа детального равновесия для нахождения функции распределения молекул идеального газа по скоростям, находящегося в состоянии термодинамического равновесия в отсутствии внешнего поля. Этот вывод был впервые предложен в 1866 году английским физиком Джеймсом Клерком Максвеллом (1831 - 1879). Для простоты будем считать, что молекулы газа представляют собой упругие шары, и при их соударении выполняются законы сохранения импульса и кинетической энергии:
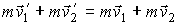 , , | (5.24) |
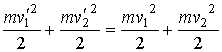 , , | (5.25) |
где 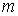 - масса молекулы.
Далее будем считать начальные скорости молекул 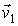 и 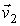 статистически независимыми друг от друга. Данное предположение является достаточно обоснованным для рассматриваемого случая хаотического движения молекул идеального газа. Вероятность того, что при столкновении молекул их скорости станут равными 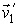 и 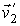 определяется вероятностью наличия у них перед столкновением скоростей 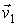 и 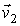 . Эта вероятность, в соответствии с формулами (5.9) и (5.10), может быть определена следующим образом:
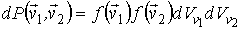 , , | (5.26) |
где: 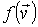 - искомая функция распределения молекул газа по скоростям, 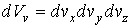 - элементарный объем в пространстве скоростей. В пространстве скоростей координаты молекулы задаются значениями проекций её скорости 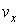 , 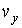 и 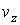 , которые откладываются по соответствующим осям прямоугольной системы координат (см. параграф 5.4).
Соответственно вероятность обратного процесса определяется вероятностью того, что в начале этого процесса скорости молекул имели значения 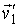 и 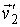 :
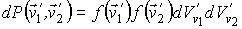 . . | (5.27) |
В соответствии с принципом детального равновесия вероятность прямого и обратного процессов должна быть одинакова:
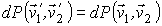 | (5.28) |
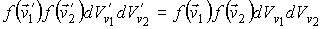 . . | (5.29) |
Рассмотрим более подробно процесс соударения двух шаров, который для упрощения рисунка схематически изображен на рис. 5.2 в двумерной системе координат. Для определенности будем считать, что ось 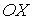 направлена по линии, соединяющей центры шаров в момент удара. | Рис. 5.2.
Схема соударения шаров |
При абсолютно упругом соударении двух одинаковых шаров они обмениваются значениями проекций их скоростей на ось, параллельную линии, соединяющей их центры (в данном случае на ось 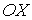 ), и сохраняют значения проекций скоростей на другие оси 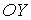 и 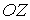 :
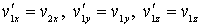 , , | (5.30) |
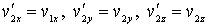 . . | (5.31) |
Отсюда следует, что и дифференциалы от соответствующих проекций скоростей должны преобразовываться по аналогичным формулам:
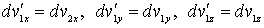 , , | (5.32) |
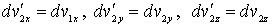 . . | (5.33) |
Перемножение всех этих выражений дает
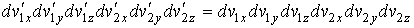 | (5.34) |
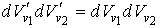 . . | (5.35) |
С учетом этой формулы выражение (5.29) принимает вид
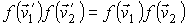 . . | (5.36) |
Полученное соотношение (5.36) является исходным для построения функции распределения по скоростям для газа, находящегося в состоянии термодинамического равновесия. Причем, указанное соотношение справедливо не только для рассмотренного модельного случая молекул в виде упругих шаров, но и для молекул произвольной формы. Это связано с тем, что оно может быть доказано на основе обратимости во времени законов механики.
При проведении дальнейших преобразований учтем свойство симметрии функции распределения по отношению к изменению направления скорости молекулы 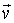 на противоположное:
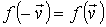 , , | (5.37) |
которое связано с равноправностью положительных и отрицательных направлений осей в пространстве. Отсюда следует, что функция 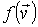 должна зависеть только от величины скорости молекулы и не зависеть от направления вектора её скорости. По этой причине далее в выражениях для функции распределения будем опускать значок вектора над скоростью молекулы.
Прологарифмируем выражение (5.36)
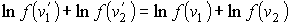 | (5.38) |
и сравним полученное выражение с формулой, являющейся следствием закона сохранения кинетической энергии (5.25):
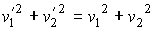 . . | (5.39) |
Сопоставление выражений (5.38) и (5.39) с учетом требования симметрии функции распределения (5.37) приводит к однозначному виду для искомой функции распределения:
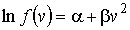 | (5.40) |
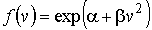 , , | (5.41) |
где постоянные 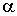 и 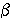 должны определяться из дополнительных физических соображений.
В заключении необходимо отметить, что принцип детального равновесия позволяет не только определять вид равновесных функций распределения для газов, описываемых классической механикой, но и применим для описания квантовомеханических систем, в частности, электронного газа.
|