5.1. Функция распределения
В качестве основной функции, применяемой при статистическом методе описания, выступает функция распределения, которая определяет статистические характеристики рассматриваемой системы. Знание её изменения с течением времени позволяет описывать поведение системы со временем. Функция распределения дает возможность рассчитывать все наблюдаемые термодинамические параметры системы.
Для введения понятия функции распределения сначала рассмотрим какую-либо макроскопическую систему, состояние которой описывается некоторым параметром 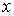 , принимающим 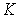 дискретных значений: 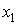 , 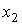 , 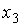 ,..., 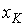 . Пусть при проведении над системой 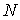 измерений были получены следующие результаты: значение 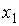 наблюдалось при 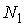 измерениях, значение 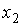 наблюдалось соответственно при 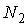 измерениях и т.д. При этом, очевидно, что общее число измерений 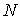 равняется сумме всех измерений 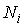 , в которых были получены значения 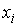 : 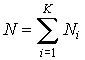 .
Увеличение числа проведенных экспериментов до бесконечности приводит к стремлению отношения 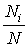 к пределу
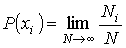 . . | (5.1) |
Вероятность 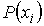 представляет собой величину, которая может принимать значения в интервале 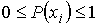 . Значение 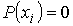 соответствует случаю, когда ни при одном измерении не наблюдается значение 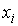 и, следовательно, система не может иметь состояние, характеризующееся параметром 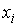 . Соответственно вероятность 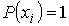 возможна только, если при всех измерениях наблюдалось только значение 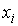 . В этом случае, система находится в детерминированном состоянии с параметром 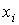 .
Сумма вероятностей 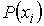 нахождения системы во всех состояниях с параметрами 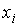 равна единице:
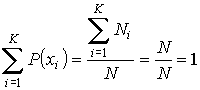 . . | (5.2) |
Условие (5.2) указывает на достаточно очевидный факт, что если набор возможных дискретных значений 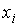 , 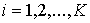 , является полным (то есть включает все возможные значения параметра 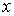 в соответствии с условиями физической задачи), то при любых измерениях параметра 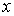 должны наблюдаться значения этого параметра только из указанного набора 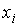 .
Рассмотренный нами случай, когда параметр, характеризующий систему, принимает набор дискретных значений не является типичным при описании макроскопических термодинамических систем. Действительно, такие параметры как температура, давление, внутренняя энергия и т.д., обычно принимают непрерывный ряд значений. Аналогично и переменные, характеризующие движение микрочастиц (координата и скорость), изменяются для систем, описываемых классической механикой, непрерывным образом.
Поэтому рассмотрим статистическое описание, применимое для случая, когда измеренный параметр 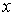 может иметь любые значения в некотором интервале 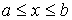 . Причем, указанный интервал может быть и не ограниченным какими либо конечными значениями 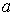 и 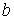 . В частности параметр 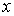 в принципе может изменяться от 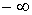 до 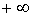 , как, например, координаты молекулы газа для случая неограниченной среды.
Пусть в результате измерений было установлено, что величина 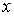 с вероятностью 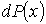 попадает в интервал значений от 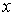 до 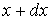 . Тогда можно ввести функцию 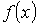 , характеризующую плотность распределения вероятностей:
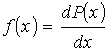 . . | (5.3) |
Функция распределения 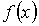 должна удовлетворять условию: 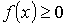 , так как вероятность попадания измеренного значения в интервал от 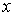 до 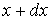 не может быть отрицательной величиной. Вероятность того, что измеренное значение попадет в интервал 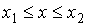 равна
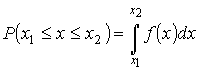 . . | (5.4) |
Соответственно, вероятность попадания измеренного значения в весь интервал возможных значений 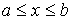 равна единице:
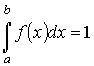 . . | (5.5) |
Функция распределения 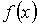 позволяет определить среднее значение любой функции 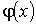 :
 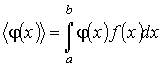 . . | (5.6) |
В частности по формуле (5.6) может быть найдено среднее значение параметра 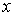 :
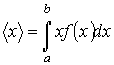 . . | (5.7) |
Если состояние системы характеризуется двумя параметрами 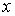 и 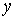 , то вероятность её нахождения в состоянии со значениями этих параметров в интервалах 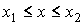 и 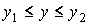 соответственно равна
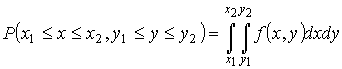 , , | (5.8) |
где 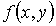 - двумерная функция распределения. Примером такой функции может служить совместное распределение для координат и скоростей молекул газа.
Соответственно для бесконечно малых интервалов 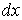 и 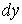 вероятность 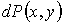 можно представить в виде
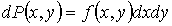 . . | (5.9) |
В случае статистической независимости значений параметров 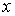 и 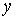 друг от друга двумерная функция распределений 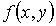 равна произведению функций распределения 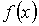 и 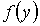 :
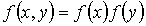 . . | (5.10) |
Это свойство функций распределения будет нами использовано при рассмотрении распределения Максвелла-Больцмана.
Задача 5.1. Найти функцию распределения и среднее значение координаты 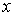 молекулы газа, находящегося в равновесном состоянии в изолированной системе при отсутствии внешних сил. Считать, что молекула может находиться только в интервале координат молекулы газа, находящегося в равновесном состоянии в изолированной системе при отсутствии внешних сил. Считать, что молекула может находиться только в интервале координат 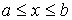 . Распространить полученный результат на трехмерный случай. . Распространить полученный результат на трехмерный случай.
Решение: Так как газ находится в равновесном состоянии, то вероятность 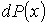 нахождения молекулы в любом интервале нахождения молекулы в любом интервале 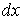 значений координаты значений координаты 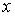 будет одинаковой и, следовательно, функция распределения будет одинаковой и, следовательно, функция распределения 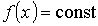 . Тогда в соответствии с условием нормировки (5.5) имеем выражение для функции распределения в интервале значений . Тогда в соответствии с условием нормировки (5.5) имеем выражение для функции распределения в интервале значений 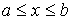 : :
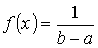 .
При 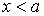 или или 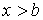 функция распределения функция распределения 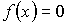 . .
Подстановка этого выражения для функции распределения 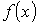 в формулу (5.7) дает среднее значение координаты в формулу (5.7) дает среднее значение координаты 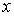 молекулы газа: молекулы газа:
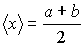 .
Полученные выражения позволяют, с использованием условия независимости переменных 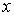 , , 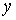 и и 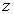 , аналогично формуле (5.10) записать выражение для трехмерной функции распределения , аналогично формуле (5.10) записать выражение для трехмерной функции распределения
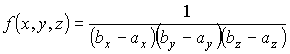 .
Соответственно средние значения координат 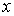 , , 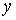 и и 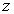 будут иметь вид: будут иметь вид:
|