| |
 |
| ГЛАВА 4. Описание термодинамических процессов |
 |
|
 |
|
| |
 |
4.1. Основное неравенство и основное уравнение термодинамики
Согласно второму началу термодинамики, элементарное количество теплоты 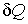 связано с изменением энтропии системы 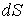 следующим неравенством (см. формулу (3.59)):
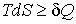 . . | (4.1) |
Совместно с первым началом термодинамики
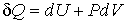 , , | (4.2) |
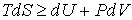 . . | (4.3) |
В этом выражении знак равенства соответствует равновесным термодинамическим процессам, а знак неравенства - неравновесным.
Для анализа равновесных процессов выражение (4.3) может быть записано в виде уравнения
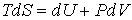 , , | (4.4) |
Рассмотрим применение этого уравнения для определения соотношения между уравнением состояния 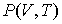 и выражением для внутренней энергии 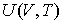 термодинамической системы. Преобразуем выражение (4.4) к следующему виду:
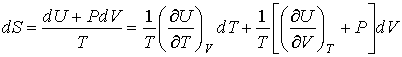 . . | (4.5) |
Здесь учтено, что внутренняя энергия  является функцией состояния, и поэтому она имеет полный дифференциал:
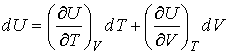 . . | (4.6) |
С другой стороны, так как энтропия 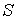 тоже является функцией состояния, для ее полного дифференциала можно записать выражение:
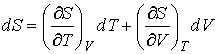 . . | (4.7) |
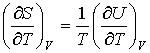 , , | (4.8) |
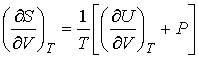 . . | (4.9) |
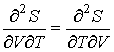 | (4.10) |
и дифференцируя по  выражение (4.8) и по 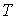 выражение (4.9), имеем:
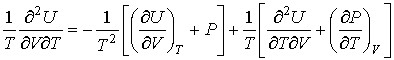 . . | (4.11) |
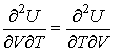 | (4.12) |
позволяет получить окончательное выражение для дифференциального уравнения, связывающего уравнение состояния 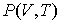 и внутреннюю энергию 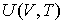 термодинамической системы
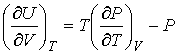 . . | (4.13) |
Рассмотрим применение этого уравнения для определения внутренней энергии идеального газа, для которого уравнение состояния имеет вид
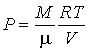 . . | (4.14) |
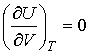 . . | (4.15) |
Таким образом, внутренняя энергия идеального газа не зависит от его объема, а является функцией только его температуры:
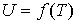 . . | (4.16) |
Так как внутренняя энергия идеального газа пропорциональна количеству вещества 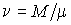 , а его молярная теплоемкость 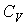 не зависит от температуры, то с точностью до произвольной постоянной имеем
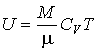 . . | (4.17) |
Подстановка полученного выражения для внутренней энергии идеального газа и его уравнения состояния в основное уравнение термодинамики равновесных процессов, записанного в виде (4.5), дает
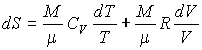 . . | (4.18) |
Интегрирование этого уравнения позволяет определить зависимость энтропии идеального газа от его объема и температуры 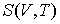 :
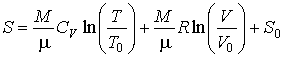 , , | (4.19) |
где: 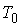 , 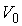 и  - константы, имеющие размерности температуры, объема и энтропии соответственно.
Выражение (4.19) полностью совпадает с формулой (3.65). Оно позволяет рассчитывать энтропию идеального газа при достаточно высоких температурах.
Задача 4.1. Определить выражение для внутренней энергии и энтропию одного моля газа Ван-дер-Ваальса, уравнение состояния которого имеет вид: 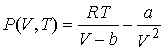 .
Решение: Подставляя уравнение состояния газа Ван-дер-Ваальса в формулу (4.13) имеем
 .
Интегрирование этого выражения дает
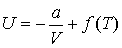 ,
где  - функция температуры. С учетом того, что при - функция температуры. С учетом того, что при 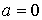 выражение для внутренней энергии газа Ван-дер-Ваальса должно совпадать с формулой (4.17), имеем выражение для внутренней энергии одного моля газа Ван-дер-Ваальса (см. формулу (2.136)) выражение для внутренней энергии газа Ван-дер-Ваальса должно совпадать с формулой (4.17), имеем выражение для внутренней энергии одного моля газа Ван-дер-Ваальса (см. формулу (2.136))
 .
Для определения энтропии одного моля газа Ван-дер-Ваальса подставим его уравнение состояния и выражение для внутренней энергии в формулу (4.5)
 ,
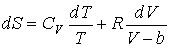 .
Интегрирование этого уравнения позволяет найти выражение для энтропии одного моля газа Ван-дер-Ваальса:
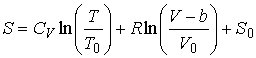 .
Из этой формулы следует, что в соответствии с третьим началом термодинамики, уравнение Ван-дер-Ваальса не применимо при  , так как при расчете энтропии по полученной формуле имеем: , так как при расчете энтропии по полученной формуле имеем:  . .
Задача 4.2. Определить выражение для внутренней энергии и энтропию фотонного газа, уравнение состояния которого имеет вид: 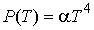 .
Решение: В соответствии с формулой (4.13) имеем:
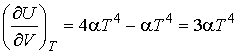 .
Следовательно, внутренняя энергия фотонного газа равна:
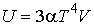 .
Здесь учтено, что при  внутренняя энергия фотонного газа также должна стремиться к нулю, и поэтому произвольная постоянная интегрирования принята равной нулю. внутренняя энергия фотонного газа также должна стремиться к нулю, и поэтому произвольная постоянная интегрирования принята равной нулю.
Отметим, что фотонный газ, в отличие от идеального газа, представляет собой термодинамическую систему с переменным числом частиц. Поэтому изменение температуры и объема, приводящие к изменению его внутренней энергии, приводят одновременно и к изменению числа частиц.
Определим энтропию фотонного газа. Согласно (4.5) имеем:
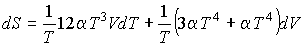 ,
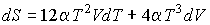 .
Это уравнение можно записать в виде
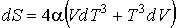 .
Тогда с учетом правила дифференцирования произведения двух функций имеем
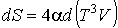 .
Интегрирование этого уравнения дает выражение для энтропии фотонного газа
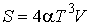 .
В этой формуле произвольная константа интегрирования принята равной нулю в соответствии с третьим началом термодинамики.
Отметим, что уравнение состояния фотонного газа  применимо при описании его состояния в случае применимо при описании его состояния в случае  . В этом заключается его принципиальное отличие от уравнения Клапейрона-Менделеева для идеального газа и уравнения Ван-дер-Ваальса для реального газа, применение которых в случае . В этом заключается его принципиальное отличие от уравнения Клапейрона-Менделеева для идеального газа и уравнения Ван-дер-Ваальса для реального газа, применение которых в случае 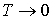 невозможно. невозможно.
|
 |
|
| |
 |
 |
| | |
|
 |
|
 |
 |
|
|