2.7. Газ Ван-дер-Ваальса
Уравнение Клапейрона-Менделеева достаточно хорошо описывает газ при высоких температурах и низких давлениях, когда он находится в условиях достаточно далёких от условий конденсации. Однако для реального газа это не всегда выполняется и тогда приходится учитывать потенциальную энергию взаимодействия молекул газа между собой. Простейшим уравнением состояния, описывающим неидеальный газ, является уравнение, предложенное в 1873 г. Иоханнесом Дидериком Ван-дер-Ваальсом (1837 - 1923):
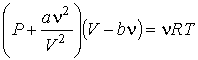 , , | (2.117) |
где: 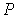 , 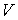 и 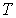 - давление, объём и температура газа, 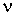 - количество молей газа, 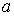 и 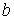 - постоянные для данного газа. Для различных газов постоянные 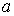 и 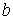 различны, и их можно определить экспериментально. Значение константы  такое же, как и для идеального газа. Такой вид уравнения состояния реального газа имеет как экспериментальные, так и молекулярно-кинетические обоснования. Остановимся сначала на последних.
Пусть на молекулы газа действуют силы притяжения и отталкивания. И те, и другие силы действуют на небольших расстояниях, но силы притяжения убывают медленнее сил отталкивания. Силы притяжения относятся к взаимодействию молекулы с её ближайшим окружением, а сила отталкивания - проявляется в момент столкновения двух молекул.
Силы притяжения внутри газа в среднем скомпенсированы для каждой отдельной молекулы. На молекулы, расположенные в тонком слое вблизи стенки сосуда, действует сила притяжения со стороны других молекул, направленная внутрь газа, которая создает давление, добавочное к создаваемому самой стенкой. Это давление иногда называют внутренним давлением.
Суммарная сила внутреннего давления, действующая на элемент поверхностного слоя газа должна быть пропорциональна числу молекул газа в этом элементе и также числу молекул в слое газа, непосредственно примыкающему к рассматриваемому элементу поверхностного слоя. Толщина этих слоёв определяется радиусом действия сил притяжения и имеет тот же порядок величины. При увеличении концентрации молекул газа в  раз, сила притяжения, приходящаяся на единицу площади приповерхностного слоя, возрастёт в 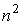 раз. Поэтому величина внутреннего давления растёт пропорционально квадрату концентрации молекул газа. Тогда для суммарного давления внутри газа  можно записать:
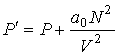 , , | (2.118) |
где:  - давление газа, которое действует на стенку сосуда (по третьему закону Ньютона стенка действует на газ с тем же давлением),  - постоянная, определяемая физико-химическими характеристиками молекул газа, 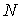 - число молекул газа в объеме  . Отношение 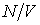 представляет собой концентрацию молекул газа. Величина 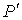 - это давление, которое создавал бы идеальный газ при тех же условиях.
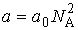 , , | (2.119) |
где: 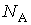 - постоянная Авогадро, имеем
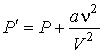 . . | (2.120) |
Итак, нами получен вид поправки к давлению, которая необходима для того, чтобы учесть слабые силы притяжения в реальном газе, отличающие его от идеального. При этом в формуле для нахождения суммарного давления внутри газа 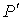 появилась новая постоянная 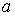 , зависящая от свойств газа.
Рассмотрим теперь поправку, связанную с действием сил отталкивания. Поскольку нами будут учитываться только парные взаимодействия между молекулами, то эта сила, в отличие от силы притяжения, не будет зависеть от концентрации молекул. По этой же причине сила отталкивания проявляется во всём объёме газа, а не только в приповерхностном слое. Зависимость этой силы от расстояния между молекулами определяет эффективное сечение взаимодействия молекул, то есть, по сути, их размеры.
Таким образом, в случае проявления короткодействующих сил отталкивания, невозможно аппроксимировать молекулы материальными точками и пренебречь их размерами. Поэтому необходимо ввести поправку, учитывающую объём, занимаемый молекулами. Её величина будет пропорциональна общему числу молекул  , а также зависеть от их физико-химических свойств. Тогда свободный от молекул объем  можно определить следующим образом:
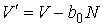 , , | (2.121) |
где:  - коэффициент, определяемый свойствами молекул. Вводя обозначение
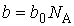 | (2.122) |
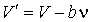 . . | (2.123) |
Величину 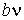 и, таким образом, величину эффективного объёма, занимаемого молекулами, нельзя получить из простых механических моделей, так как сами размеры молекул определяются характером сил отталкивания. Поскольку уравнение Ван-дер-Ваальса является по сути своей эмпирическим, коэффициент 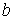 , так же как и коэффициент 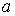 , должны определяться в первую очередь экспериментально.
Если теперь в левой части уравнения Клапейрона-Менделеева (2.2):
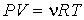 | (2.124) |
произвести замену произведения 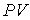 на произведение
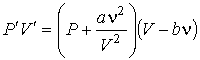 , , | (2.125) |
то получится уравнение Ван-дер-Ваальса (2.117).
Отметим, что проводить замену объема 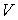 на  в формуле (2.120) для давления 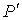 нет необходимости, так как константы  и  достаточно малы. Например, для азота и кислорода 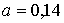 Н*м 4/моль 2. Коэффициент 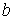 для азота и кислорода соответственно имеет значения: 39*10 -6 м 3/моль и 32*10 -6 м 3/моль.
Введение поправки, обусловленной действием сил притяжения, привело к тому, что уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня. Для уравнения Ван-дер-Ваальса имеют место два следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный.
На рис. 2.8 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур. | Рис. 2.8.
Изотермы газа Ван-дер-Ваальса |
На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма 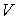 при одинаковых значениях параметров  и 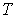 . Это соответствует существованию трёх действительных корней уравнения (2.117). При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения  , 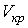 и 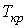 в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения (2.117). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями 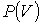 .
Критические параметры  ,  и  можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба:
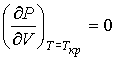 , , | (2.126) |
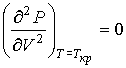 . . | (2.127) |
Решая эти два уравнения совместно с (2.117) можно получить
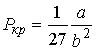 , , | (2.128) |
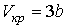 , , | (2.129) |
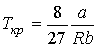 . . | (2.130) |
Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами  ,  и  , величина которых зависит от свойств газа.
Обратимся теперь к экспериментальным обоснованиям уравнения состояния газа Ван-дер-Ваальса. На рис 2.9 показан вид экспериментально полученных изотерм, характерный для многих веществ. | Рис. 2.9.
Изотермы реального газа |
На этих кривых виден горизонтальный участок, который заменяет немонотонный участок на изотермах газа Ван-дер-Ваальса. Справа от горизонтального участка экспериментальная изотерма монотонно растет с уменьшением объема, что соответствует сжатию реального газа при постоянной температуре. Горизонтальный участок соответствует сжижению газа, которое при заданной температуре происходит при постоянном давлении. При этом существует двухфазная система жидкость-газ. Наконец, слева от горизонтального участка, где изотерма вновь становится монотонно убывающей функцией  , весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема. Это связано с тем, что размеры молекул жидкостей становятся сравнимы с межмолекулярными расстояниями. Этот участок экспериментальных изотерм наиболее сильно отличается от предсказываемого уравнением для газа Ван-дер-Ваальса.
Экспериментально изотермы могут быть получены при изотермическом сжатии газа в системе, состоящей из сосуда с поршнем, соединенного с манометром. Семейство изотерм для углекислого газа было построено Томасом Эндрюсом (1813 - 1885) во второй половине XIX века. Им было установлено, что при температуре выше 31,1 oC углекислота продолжает оставаться газообразной при любом давлении. При более низкой температуре углекислый газ при сильном сжатии переходил в жидкое состояние.
В первой половине XIX века предполагали существование абсолютных газов, которые не могут быть сжижены ни при каких условиях. Однако опыт показал, что любое вещество может быть сжижено при достаточно высоком давлении и низкой температуре.
Совокупность участков изотерм реального газа, соответствующих двухфазным системам жидкость-газ, образуют колоколообразную фигуру (см. рис. 2.9), вершиной которой является критическая точка. При температурах выше критической вещество может существовать только в газообразном состоянии. При температуре ниже критической, вещество может быть сжижено. Критическая температура для гелия очень низкая - 5,2 К. Поэтому долгое время его считали абсолютным газом.
В отличие от гелия, водорода, кислорода и азота, чьи критические температуры достаточно низкие, такие вещества как вода и ртуть (критические температуры 647 К и 1820 К соответственно) существуют как в жидком, так и в газообразном состояниях при комнатных температурах. Поэтому возникли такие термины как "водяной пар" и "пары ртути". Сегодня, с исчезновением понятия "абсолютный газ" исчезло различие понятий "газ" и "пар".
Для нахождения внутренней энергии газа Ван-дер-Ваальса, воспользуемся следующим приемом. Пусть над газом Ван-дер-Ваальса осуществляется процесс без теплообмена с окружающей средой. Тогда изменение его внутренней энергии можно записать в виде
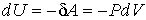 . . | (2.131) |
При тех же условиях изменение внутренней энергии идеального газа можно было бы рассчитать по формуле
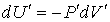 . . | (2.132) |
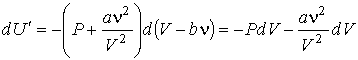 . . | (2.133) |
Первое слагаемое в правой части выражения (2.133) согласно формуле (2.131) представляет собой изменение внутренней энергии газа Ван-дер-Ваальса.
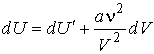 . . | (2.134) |
Интегрирование этого выражения дает
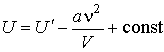 . . | (2.135) |
Здесь произвольную константу интегрирования необходимо положить равной нулю, так как при 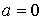 выражения для внутренних энергий газа Ван-дер-Ваальса и идеального газа должна совпадать: 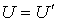 .
Использование выражения (2.64) для внутренней энергии идеального газа позволяет записать формулу, для расчета внутренней энергии газа Ван-дер-Ваальса в виде
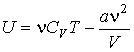 . . | (2.136) |
Как следует из этого выражения, внутренняя энергия газа Ван-дер-Ваальса зависит не только от его температуры, как в случае с идеальным газом, но и от объема, занимаемого им. По этой причине, при осуществлении изотермических процессов в газе Ван-дер-Ваальса, будет изменяться его внутренняя энергия, а, следовательно, при таких процессах подведенная к газу теплота не будет равна совершенной им работе.
Если внутренняя энергия идеального газа определяется кинетической энергией его молекул, то для газа Ван-дер-Ваальса существенное значение имеет потенциальная энергия, обусловленная силами притяжения и отталкивания. Согласно первому началу термодинамики изменение внутренней энергии газа может быть осуществлено либо сообщением ему теплоты, либо совершением над ним механической работы. Если газ адиабатически расширяется, не совершая механической работы, его внутренняя энергия остается неизменной. Для идеального газа неизменность внутренней энергии эквивалентна постоянству температуры газа, что было показано в описанных выше опытах Гей-Люссака.
В экспериментах, проведенных Джоулем и Томсоном на реальных газах, было установлено, что при адиабатическом расширении их температура изменяется, причем может, как повышаться, так и понижаться. Это явление получило название эффекта Джоуля-Томсона. Объясняется этот эффект тем, что в силу закона сохранения энергии, уменьшение кинетической энергии реального газа равно приращению его потенциальной энергии. Если потенциальная энергия взаимодействия молекул реального газа при расширении возрастает, то его температура при этом падает. Если потенциальная энергия уменьшается, то его температура растет. В частности, для газа Ван-дер-Ваальса, если силы притяжения играют более существенную роль, чем силы отталкивания, то газ при расширении охлаждается, а если силы отталкивания превосходят силы притяжения, то его температура увеличивается. Подробный анализ эффекта Джоуля-Томсона выполнен в параграфе 4.3.
Практическое применение эффекта Джоуля-Томсона связано в первую очередь с охлаждением газов и ожижением их. В конце XIX века Карлом Линде (1842 - 1934) была разработана машина для ожижения воздуха, в которой охлажденный вследствие эффекта Джоуля-Томсона воздух осуществляет предварительное охлаждение следующей порции воздуха, которая затем в свою очередь расширяется с уменьшением температуры. Повторяя процесс многократно, можно получить температуру воздуха ниже критической, и ожижить его. Используя эту схему, нидерландский физик Гейке Камерлинг-Оннес (1853 - 1926) в 1908 году получил жидкий гелий, что стало началом новой области физики - физики низких температур.
Для получения жидкого гелия потребовалось предварительно охладить его жидким водородом. Для получения жидкого водорода также потребовалось его предварительное охлаждение жидким воздухом. Это объясняется тем, что расширение сжатых (как правило, до нескольких десятков атмосфер) гелия и водорода при комнатной температуре сопровождается увеличением их температуры. Предварительное охлаждение позволяет перевести их в состояние, при котором адиабатическое расширение приводит к их охлаждению.
В 30-е годы XX столетия советским физиком Петром Леонидовичем Капицей (1894 - 1984) был разработан более эффективный способ получения сжиженных газов, основанный на том, что газ при адиабатическом расширении совершает положительную работу, то есть его внутренняя энергия уменьшается. Созданное Капицей устройство называется турбодетандером. В нем газ совершает работу при вращении теплоизолированной турбины.
Задача 2.7. Оценить коэффициент  газа Ван-дер-Ваальса, если эффективный размер молекул газа газа Ван-дер-Ваальса, если эффективный размер молекул газа 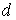 , а объем, занимаемый , а объем, занимаемый 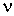 молями газа, равен молями газа, равен 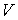 . Длина свободного пробега молекул идеального газа при тех же условиях равна . Длина свободного пробега молекул идеального газа при тех же условиях равна 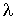 . .
Решение: Так как в соответствии с формулой (2.50) длина свободного пробега обратно пропорциональна концентрации: 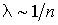 , а в соответствии с основным уравнением молекулярно-кинетической теории (2.32) , а в соответствии с основным уравнением молекулярно-кинетической теории (2.32)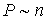 , имеем: , имеем:  . Обратно пропорциональная зависимость связана с тем, что количество ударов молекул газа о стенку, а, следовательно, и давление газа возрастают с уменьшением длины свободного пробега. . Обратно пропорциональная зависимость связана с тем, что количество ударов молекул газа о стенку, а, следовательно, и давление газа возрастают с уменьшением длины свободного пробега.
Длину свободного пробега 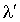 для молекул газа Ван-дер-Ваальса можно оценить как для молекул газа Ван-дер-Ваальса можно оценить как  . Тогда из установленной выше зависимости давления газа от длины свободного пробега запишем следующее соотношение: . Тогда из установленной выше зависимости давления газа от длины свободного пробега запишем следующее соотношение:
 ,
где:  - давление газа Ван-дер-Ваальса, - давление газа Ван-дер-Ваальса, 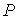 - давление идеального газа при том же объеме и той же температуре. Считая, что - давление идеального газа при том же объеме и той же температуре. Считая, что 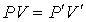 , где , где 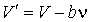 , имеем: , имеем:
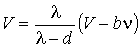 .
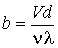 .
Так как величина 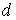 для газов обычно много меньше для газов обычно много меньше 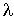 , то коэффициент , то коэффициент 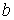 достаточно мал. достаточно мал.
|