2.2. Основные положения молекулярно-кинетической теории
Метод описания свойств сложных объектов, например термодинамических систем, через свойства элементарных их составляющих, был впервые использован в древней Греции. Этот метод применяется в механике, где в качестве элементарного объекта используется материальная точка. При описании различных веществ в качестве их элементарных составляющих древними греками было введено понятие атома. Это название происходит от греческого слова, означающего неделимый. В физике нашли широкое применение такие элементарные объекты как точечные заряды, ядра, элементарные частицы, кварки и т.д.
Молекулярно-кинетическая теория развивалась параллельно с термодинамикой, и зачастую эти теории разрабатывались одними и теми же исследователями. При этом молекулярно-кинетическая теория позволяла получить обоснование термодинамических законов и более глубоко объяснить их физическую сущность.
Очевидно, что сформулированные выше требования выполняются для достаточно (но не очень сильно) разреженных газов, молекулы которых не вступают в химические взаимодействия между собой.
Далее будем предполагать, что рассматриваемый газ находится в состоянии термодинамического равновесия со стенками сосуда, и взаимодействие его молекул со стенками описывается моделью упругих соударений с зеркальным отражением.
Покажем, что молекулярно-кинетическая теория позволяет получить для идеального газа закон Бойля-Мариотта и сделать вывод о связи кинетической энергии его молекул с температурой газа. Рассмотрим сосуд в виде куба с ребром длиной 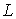 , а оси координат 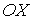 ,  и 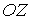 направим параллельно трем ребрам куба (см. рис. 2.1). | Рис. 2.1.
Схема упругих соударений молекул идеального газа:
1 - со стенкой, расположенной в плоскости YOZ,
2 – со стенкой, расположенной в плоскости XOZ ,
3 – двух одинаковых молекул между собой |
Если молекула массой 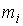 , имеющая составляющую скорости 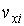 (на рис. 2.1 индекс  при скоростях опущен) вдоль оси  , сталкивается со стенкой сосуда, расположенной в плоскости 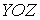 , то этой стенке будем передан импульс:
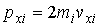 . . | (2.15) |
Считая, что молекула, летящая вдоль оси  , не испытывает соударений с другими молекулами газа, оценим промежуток времени  между очередными соударениями этой молекулы со стенкой сосуда, после её переотражения от противоположной его стенки:
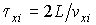 . . | (2.16) |
Полученное выражение применимо и для более общего случая, так как при упругом соударении рассматриваемой молекулы с другими стенками сосуда, например со стенкой, расположенной в плоскости 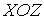 , составляющая её скорости вдоль оси 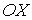 не изменяется, а при упругом соударении двух одинаковых молекул происходит обмен их скоростями (см. рис. 2.1).
Тогда силу 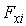 и давление 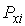 , действующие со стороны рассматриваемой молекулы на стенку сосуда, расположенную в плоскости 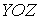 , можно рассчитать по следующим формулам:
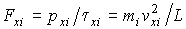 , , | (2.17) |
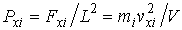 , , | (2.18) |
где:  - объем, занимаемый газом внутри сосуда.
Рассуждая аналогичным образом, величины давлений, действующих со стороны молекулы на стенки, лежащие в плоскостях 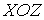 и 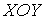 , можно определить с помощью формул:
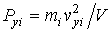 , , | (2.19) |
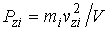 . . | (2.20) |
Предполагая газ изотропным, можно считать, что значения величин давлений на различные стенки сосуда в среднем одинаковы:
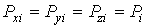 . . | (2.21) |
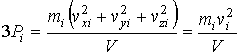 , , | (2.22) |
где: 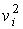 - значение квадрата скорости  -ой молекулы.
Выражение (2.22) позволяет получить зависимость между давлением и кинетической энергией  для 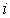 -ой молекулы:
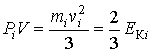 . . | (2.23) |
Для нахождения уравнения для полного давления  необходимо просуммировать выражение (2.23) по всем молекулам газа:
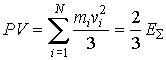 , , | (2.24) |
где:  - полное число молекул, 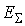 - суммарная кинетическая энергия поступательного движения всех молекул газа.
Если суммарная кинетическая энергия идеального газа постоянна:  , то на основании выражения (2.24) можно записать уравнение
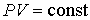 , , | (2.25) |
полностью совпадающие с выражением (2.11), описывающим закон Бойля-Мариотта.
Сравнение выражения (2.24) с уравнением Клапейрона-Менделеева (2.2) позволяет сделать вывод, что для идеального газа кинетическая энергия поступательного движения его молекул пропорциональна абсолютной температуре этого газа:
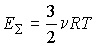 . . | (2.26) |
Для одного моля газа имеем:
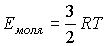 . . | (2.27) |
Полученные выражения позволяют утверждать, что абсолютная температура идеального газа есть мера кинетической энергии поступательного движения его молекул. Поскольку у идеального газа отсутствует потенциальная энергия взаимодействия молекул между собой, то их суммарную кинетическую энергию можно считать равной внутренней энергии идеального газа. Поэтому, температура также является мерой внутренней энергии идеального газа в состоянии термодинамического равновесия.
Среднюю кинетическую энергию поступательного движения одной молекулы газа 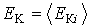 можно найти как отношение суммарной кинетической энергии молекул 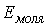 , содержащихся в одном моле газа, к постоянной Авогадро  , численно равной количеству этих молекул:
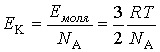 . . | (2.28) |
Или, если ввести новую постоянную:
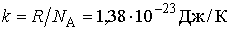 , , | (2.29) |
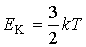 . . | (2.30) |
С помощью формулы (2.29) уравнение Клапейрона-Менделеева (2.2) может быть преобразовано к виду:
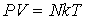 , , | (2.31) |
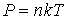 , , | (2.32) |
или с использованием формулы (2.30)
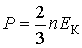 . . | (2.33) |
Здесь: 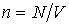 - концентрация молекул газа.
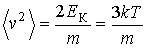 | (2.34) |
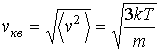 . . | (2.35) |
В соответствие с формулами (2.8) и (2.29) постоянную Больцмана можно представить в виде:
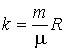 . . | (2.36) |
Тогда выражение (2.35) для средней квадратичной скорости можно записать в форме:
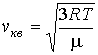 . . | (2.37) |
Уравнение (2.32) позволяет определить давление смеси газов. Из него следует, что давление, создаваемое идеальным газом, не зависит от физико-химических свойств молекул, образующих газ. Считая газы находящимися в равновесном состоянии, концентрацию молекул в смеси  можно представить как сумму концентраций молекул всех газов 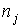 , входящих в смесь:
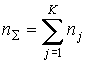 , , | (2.38) |
где 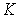 - число газов в смеси.
Использование выражения (2.32) позволяет для суммарного давления смеси газов 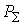 записать
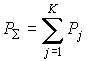 , , | (2.39) |
где  - давление 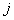 -го газа смеси.
До сих пор мы рассматривали модель идеального газа, молекулы которого считались материальными точками, то есть одноатомный газ. Для таких молекул число их степеней свободы, в соответствии с классической механикой, равняется количеству координат, необходимому для задания их положения в пространстве. Очевидно, что число координат в трехмерном пространстве, а следовательно и число степеней свободы одноатомного газа, равно трем.
Однако молекула газа не обязательно должна состоять из одного атома, который считается материальной точкой. Газ может быть двухатомным, трёхатомным и т. д. Для молекул таких газов характерно наличие внутренней структуры и, соответственно, дополнительных степеней свободы. Если атомы в молекуле жестко связаны между собой, в качестве дополнительных степеней свободы выступают вращательные степени, характеризующие угловое положение молекулы в пространстве. В этом случае двухатомные молекулы имеют дополнительно две вращательные степени свободы, так как учет вращения вокруг оси, соединяющей атомы, считающиеся материальными точками, не имеет смысла. Следовательно, для такой молекулы общее число её степеней свободы равно пяти. Для молекул, состоящих из трех и белее жестко связанных атомов, число дополнительных вращательных степеней свободы равно трем, а суммарное число степеней свободы - соответственно шести.
Если атомы в молекуле связаны не жесткой, а упругой связью, то кроме вращательных, появляются еще и колебательные степени свободы, наличие которых необходимо учитывать при описании свойств многоатомного газа, состоящего из таких молекул.
В одноатомном газе молекула имеет три степени свободы, соответствующие трем пространственным координатам. Вследствие равноправности этих координат, можно, на основании выражения (2.30), сделать предположение, что на каждую степень свободы молекулы одноатомного газа приходится в среднем кинетическая энергия, равная  .
Таким образом, в самом общем случае для определения суммарной кинетической энергии всех молекул газа 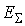 (внутренней энергии идеального газа) необходимо вместо выражения (2.26) использовать формулу:
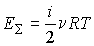 | (2.40) |
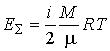 , , | (2.41) |
а для нахождения кинетической энергии одной молекулы - соответственно вместо (2.30) надо применять следующее выражение:
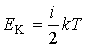 . . | (2.42) |
Здесь: 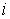 - число степеней свобода молекулы газа.
Для одноатомного газа 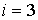 , а для газа, молекулы которого состоят из двух жестко связанных атомов  . Соответственно для газов из жестких, многоатомных молекул  .
При расчете энергии многоатомных молекул с колебательными степенями свободы необходимо, кроме кинетической энергии атомов в молекуле, учитывать потенциальную энергию взаимодействия этих атомов. Если для описания колебаний атомов в молекуле применима модель гармонического осциллятора, что, как показывает опыт, оправдано, то среднюю потенциальную энергию атомов можно считать равной их средней кинетической энергии. Тогда полную энергию, приходящуюся на одну колебательную степень свободы, можно считать равной удвоенной её кинетической энергии. Поэтому при учете колебательных степеней свободы необходимо энергию молекулы увеличивать на величину  (а число 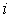 соответственно на два) на каждую колебательную степень свободы. Этим отличается учет колебательных степеней свободы от учета степеней свободы, связанных с поступательным и вращательным движением, где на каждую степень свободы приходится энергия, равная 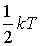 .
Отметим, что непосредственное использование выражений (2.41) и (2.42) для многоатомных газов, в молекуле которых атомы связаны не жестко, не является корректным. Это объясняется тем, что колебательные степени свободы обладают при нормальных условиях значительно меньшей, в сравнение с 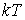 , энергией. Только при достаточно высокой температуре, порядка 10 3 К, энергия колебательных степеней свободы становится сравнима с  . При низких температурах (порядка 10 К) закон равнораспределения становится не применим и для вращательных степеней свободы. Это связано с тем, что законы классической статистической механики, на которых основано доказательство закона о равнораспределении энергии по степеням свободы, имеют весьма ограниченное применение для атомно-молекулярных систем. Здесь необходимо применение квантовомеханических законов.
Однако для газов, находящихся при нормальных условиях, закон равнораспределения может быть применён для поступательных и вращательных степеней свободы с достаточно высокой степенью точности. Этим объясняется широкое использование при практических расчетах молекулярно-кинетической теории.
Условие, что молекулы идеального газа должны гораздо чаще претерпевать взаимные столкновения по сравнению с соударениями со стенками, соответствует случаю, когда размеры сосуда существенно превышают длину свободного пробега молекул.
Для оценки длины свободного пробега молекул идеального газа, воспользуемся следующей простейшей молекулярно-кинетической моделью. Будем считать, что молекулы идеального газа представляют собой твёрдые шары, диаметром 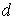 , которые взаимодействуют друг с другом только путём упругих соударений при непосредственном соприкосновении. Рассмотрим взаимодействие двух молекул, причём систему отсчёта свяжем с центром молекулы 1, расположенной слева (см. рис. 2.2). Молекулы на рисунке изображены жирными сферами. | Рис. 2.2.
Схема взаимодействия двух молекул идеального газа |
Пусть молекула 2 движется со скоростью 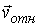 в этой системе отсчёта и проходит расстояние  с момента предыдущего столкновения до столкновения с молекулой 1. Для того, чтобы молекула 2 без столкновений прошла путь 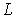 , внутри цилиндра с основанием площадью  и длиной 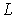 не должно быть ни одной другой молекулы газа, кроме молекулы 1. Это условие требует уточнения. Поскольку мы аппроксимируем форму молекулы как шаровую с диаметром 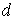 , то молекула 2 не испытает ни одного столкновения с другими молекулами, если внутри рассматриваемого цилиндра не будет ни одного их центра. Из этого следует, что на одну молекулу газа в среднем приходится объем величиной
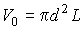 . . | (2.43) |
Так как концентрацию молекул газа 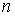 можно представить в виде
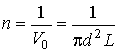 , , | (2.44) |
то отсюда следует выражение для среднего значения величины  :
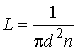 . . | (2.45) |
Если в лабораторной системе отсчёта средняя скорость молекул равна 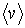 , то длина свободного пробега  и величина 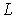 будут связаны соотношением
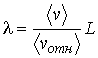 , , | (2.46) |
где: 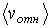 - среднее значение относительной скорости молекулы 2 в системе отсчёта, связанной с молекулой 1.
По правилу сложения векторов, величину относительной скорости молекул можно определить по формуле (см. рис. 2.3):
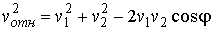 , , | (2.47) |
где:  и 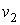 - скорости 1 и 2 молекул,  - угол между направлениями векторов этих скоростей. | Рис. 2.3.
Схема к определению относительной скорости молекул |
Так как скорости молекул могут иметь любые произвольные направления, а средние значения их величин в равновесном газе одинаковые, то усреднение соотношения (2.47) по всем возможным углам ( дает
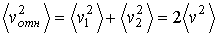 . . | (2.48) |
Соотношение (2.48) позволяет, считая, что средние квадраты скоростей молекул пропорциональны квадратам средних значений этих скоростей, записать следующее соотношение:
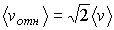 . . | (2.49) |
Тогда выражение для длины свободного пробега принимает форму
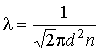 . . | (2.50) |
Из этой формулы следует обратная пропорциональная зависимость длины свободного пробега молекулы идеального газа 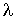 от его концентрации 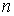 .
Часто вместо величины 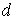 , характеризующей размер молекулы, используется величина
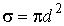 , , | (2.51) |
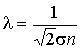 . . | (2.52) |
Определим также среднюю частоту соударений молекулы газа с другими молекулами. Эта величина равна отношению средней скорости молекулы к длине её свободного пробега:
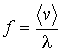 , , | (2.53) |
или с учетом выражения (2.52):
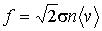 . . | (2.54) |
В заключении отметим, что полученные формулы справедливы с точностью до безразмерного множителя, величина которого порядка единицы. Это связано со сделанным выше предположением о том, что молекулы газа представляют собой твердые шара. Учет реальной формы и физических свойств молекул не приводит к принципиальным отличиям, так как размер молекулы 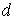 , и, следовательно, её эффективное сечение  , не могут быть точно определены с помощью независимых измерений. Экспериментальные значения этих величин достаточно сильно отличаются при использовании различных способов их измерения.
|