6.4. Динамика твердого тела
Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них - уравнение движения центра масс (4.11), другое-уравнение моментов в С-системе (6.24):
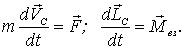 | (6.26) |
Зная законы действующих внешних сил, точки их приложения и начальные условия, можно с помощью этих уравнений найти как скорость, так и положение каждой точки твердого тела в любой момент времени, т. е. полностью решить задачу о движении тела. Однако, несмотря на кажущуюся простоту уравнений (6.26), решение их в общем случае представляет собой весьма трудную задачу. Это прежде всего обусловлено тем обстоятельством, что связь между собственным моментом импульса 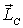 и скоростями отдельных точек твердого тела в С-системе оказывается сложной, за исключением немногих частных случаев. Мы не будем рассматривать эту задачу в общем виде (она решается в курсе теоретической механики) и ограничимся в дальнейшем только отдельными частными случаями.
Приведем некоторые соображения, прямо вытекающие из вида самих уравнений (6.26). Если перенести силы вдоль направления их действия, то ясно, что не изменятся ни их результирующая 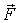 , ни их суммарный момент 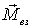 . При этом уравнения (6.26) тоже не изменятся, а следовательно не изменится и движение твердого тела. Поэтому точки приложения внешних сил можно переносить вдоль направления действия сил - удобный прием решения задач, которым постоянно пользуются.
Рассмотрим теперь понятие равнодействующей силы. В тех случаях, когда суммарный момент всех внешних сил оказывается перпендикулярным результирующей силе, т. е. 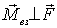 , все внешние силы могут быть сведены к одной силе 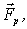 , действующей вдоль определенной прямой. В самом деле, если относительно некоторой точки О суммарный момент 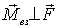 , то всегда можно найти такой вектор 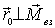 (рис. 6.14), что при заданных  и 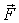
При этом выбор 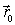 неоднозначен: прибавление к нему любого вектора 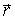 , | Рис. 6.14.
Введение понятия равнодействующей силы |
параллельного 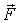 , не изменит последнего равенства. А это означает, что данное равенство определяет не точку "приложения" силы 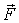 , а линию ее действия. Зная модули M и F соответствующих векторов, можно найти плечо l силы 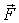 (рис.6.14): 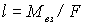 .
Таким образом, если  , систему сил, действующих на отдельные точки твердого тела, можно заменить одной равнодействующей силой - силой, которая равна результирующей 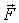 и создает момент, равный суммарному моменту 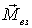 всех внешних сил.
Таким случаем является действие однородного силового поля, например поля тяжести, в котором действующая на каждую частицу сила имеет вид 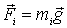 . В этом случае суммарный момент сил тяжести относительно любой точки О равен
Стоящая в круглых скобках сумма, равна 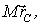 где 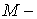 масса тела 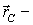 радиус-вектор его центра масс относительно точки O. Поэтому
Это означает, что равнодействующая 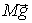 сил тяжести проходит через центр масс тела. Обычно говорят, что равнодействующая сил тяжести приложена к центру масс тела или к его центру тяжести. Ясно, что момент этой силы относительно центра масс тела равен нулю.
Теперь перейдем к рассмотрению четырех важных частных случаев движения твердого тела.
Вращение вокруг неподвижной оси.
Рассмотрим вращение твердого тела вокруг неподвижной оси. Найдем выражение для момента импульса твердого тела относительно оси 00' (рис. 6.15). Воспользовавшись формулой (6.9) запишем
где  и 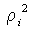 - масса и расстояние от оси вращения  частицы твердого тела,  - его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим
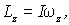 | (6.27) |
где I - так называемый момент инерции твердого тела относительно оси 00':
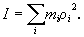 | (6.28) |
| Рис. 6.15.
Вращение твердого тела вокруг оси |
Момент инерции твердого тела зависит, как нетрудно видеть, от распределения масс относительно интересующей нас оси и является величиной аддитивной.
Вычисление момента инерции тела проводится по формуле
где dm и dV - масса и объем элемента тела, находящегося на расстоянии  от интересующей нас оси z, 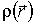 - плотность тела в данной точке.
Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в следующей таблице (здесь т - масса тела):
Вид твердого тела | Положение оси | Момент инерции 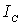 |
Тонкий стержень длины L | Перпендикулярно стержню | |
Сплошной цилиндр радиуса R | Совпадает с осью цилиндра | |
Тонкий диск радиуса R | Совпадает с диаметром диска | |
Шар радиуса R | Проходит через центр шара | |
Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси z равен моменту инерции относительно оси параллельной данной и проходящей через центр масс С тела, плюс произведение массы т тела нa квадрат расстояния а между осями:
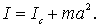 | (6.29) |
Доказательство этой теоремы приведено в приложении.
Таким образом, если известен момент инерции 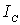 то нахождение момента инерции I элементарно.  Например, момент инерции тонкого стержня (массы т и длины l) относительно оси, перпендикулярной стержню и проходящей через его конец, равен
Запишем основное уравнение динамики вращения твердого тела с неподвижной осью вращения. Это уравнение легко получить, как следствие (6.15), если продифференцировать (6.27) по времени, тогда
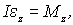 | (6.30) |
где 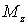 - суммарный момент всех внешних сил относительно оси вращения,  проекция углового ускорения на ось вращения. Из этого уравнения, в частности, видно, что момент инерции I определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил 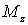 тело с большим моментом инерции приобретает меньшее угловое ускорение.
Вспомним, что моменты сил относительно оси - величины алгебраические: их знаки зависят как от выбора положительного направления оси z, совпадающей с осью вращения, так и от направления | Рис. 6.16.
Выбор положительного направления вращения (правый винт) |
"вращения" соответствующего момента силы. Например, выбрав положительное направление оси z, как показано на рис. 6.16, мы тем самым
задаем и положительное направление отсчета угла - оба эти направления связаны правилом правого винта. Полагают, что если некоторый момент "вращает" в положительном направлении угла, то он считается положительным, и наоборот. А знак суммарного момента 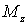 в свою очередь определяет знак  - проекции вектора углового ускорения на ось z.
Интегрирование уравнения (6.30) с учетом начальных условий -значений угловой скорости и угла 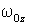 и  начальный момент времени - позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси, т. е. найти зависимость от времени угловой скорости 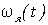 и угла поворота  .
Заметим, что уравнение (6.30) справедливо в любой системе отсчета, жестко связанной с осью вращения. Однако если система отсчета неинерциальная, то необходимо помнить, что момент сил 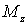 включает в себя не только моменты сил взаимодействия с другими телами, но и моменты сил инерции.
Получим выражение для кинетической энергии вращающегося твердого тела с неподвижной осью вращения. Учитывая связь скорости  частицы вращающегося твердого тела с угловой скоростью 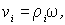 запишем
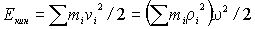 ,
 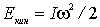 , , | (6.31) |
где I - момент инерции тела относительно оси вращения, 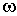 - его угловая скорость.
Пример. Диск 1 (рис.6.17) вращается вокруг гладкой вертикальной оси с угловой скоростью 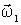 . На него падает диск 2, вращающийся с угловой скоростью 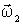 . Вследствие трения между ними оба диска через некоторое время начинают вращаться как единое целое. Найти приращение кинетической энергии вращения этой системы, если моменты инерции дисков относительно оси вращения равны соответственно 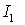 и 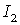 . | Рис. 6.17.
Пример определения приращения кинетической энергии |
Сначала найдем установившуюся угловую скорость вращения. Из закона сохранения момента импульса системы относительно оси z следует, что 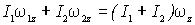 , откуда получаем
Заметим, что 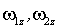 и 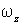 и 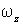 - величины алгебраические. Если окажется, что 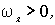 то это значит, что соответствующий вектор совпадает с положительным направлением оси z, и наоборот. Приращение кинетической энергии вращения этой системы
Заменив  его выражением, получим
Знак минус показывает, что кинетическая энергия системы уменьшается.
Обратим внимание на то, что полученные результаты весьма похожи и по форме, и по смыслу на случай абсолютно неупругого столкновения частиц.
Рассмотрим работу внешних сил при вращении твердого тела вокруг неподвижной оси. В соответствии с законом изменения механической энергии системы элементарная работа всех внешних сил, действующих на твердое тело, равна приращению только кинетической энергии тела, так как его собственная потенциальная энергия при этом не меняется. Таким образом,  . Воспользовавшись (6.31), запишем 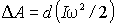 . Так как ось z совпадает с осью вращения, то 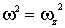 и
Но согласно (6.30)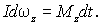 . Подставив это выражение в последнее уравнение для 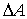 и учтя, что 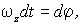 получим
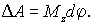 | (6.32) |
Работа  - величина алгебраическая: если 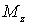 и 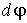 имеют одинаковые знаки, то 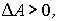 если же их знаки противоположны, то 
Работа внешних сил при повороте твердого тела на конечный угол 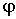 равна
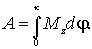 | (6.33) |
В случае, если  последнее выражение упрощается: 
Таким образом, работа внешних сил при вращении твердого тела вокруг неподвижной оси определяется моментом  этих сил относительно данной оси. Если силы таковы, что их момент 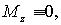 то работы они не производят.
2) Плоское движение тердого тела.
Перейдем к рассмотрению плоского движения твердого тела. При плоском движении центр масс С твердого тела движется в определенной плоскости, неподвижной в данной К-системе отсчета, а вектор его угловой скорости 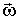 все время остается перпендикулярным этой плоскости. Последнее означает, что в С-системе твердое тело совершает чисто вращательное движение вокруг неподвижной в этой системе оси, проходящей через центр инерции тела. Вращательное же движение твердого тела определяется уравнением (6.30), которое, как было отмечено, справедливо в любой системе отсчета.
Таким образом, мы имеем следующие два уравнения, описывающие плоское движение твердого тела:
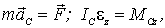 | (6.34) |
где т - масса тела, 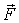 - результирующая всех внешних сил, 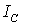 и 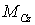 - момент инерции и суммарный момент всех внешних сил относительно оси, проходящей через центр инерции тела.
При этом следует помнить, что момент 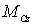 включает в себя только внешние силы взаимодействия, несмотря на то что С-система в общем случае является неинерциальной. Это связано с тем, что суммарный момент сил инерции равен нулю как относительно центра масс, так и относительно любой оси, проходящей через эту точку. Поэтому его можно просто не учитывать .
Заметим также, что угловое ускорение  , а следовательно, 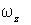 и 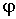 одинаковы в обеих системах отсчета, так как C-система движется поступательно относительно инерциальной K-системы отсчета.
Интегрируя уравнения (6.34) с учетом начальных условий, можно найти зависимости 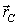 и  и, определяющие положение твердого тела в любой момент t.
При решении задачи о движении несвободного твердого тела необходимо использовать еще одно, дополнительное, условие, определяющее ограничения движения имеющимися связями. Оно дает кинематическую связь между линейным и угловым ускорениями.
Пример. Однородный цилиндр массы m и радиуса r скатывается без скольжения по наклонной плоскости, составляющей угол  с (рис.6.18). Найти уравнения движения цилиндра.
Стандартный подход к решению подобной задачи состоит в следующем. Сперва определяют силы, действующие на тело, и точки их | Рис. 6.18.
Скатывание цилиндра с наклонной плоскости |
приложения. В данном случае это 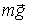 - сила тяжести, 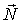 - нормальная составляющая силы реакции со стороны наклонной плоскости и  - сила трения покоя. Затем выберем положительные направления оси х и угла поворота 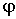 . Эти направления лучше всего взять сразу согласованными, так чтобы знаки ускорений  и 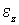 были одинаковы, например, как показано па рис.6.18, справа. После этого записывают сами уравнения движения, в проекциях па выбранные таким образом положительные направления  и 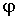 :
Кроме того, условие отсутствия скольжения определяет еще кинематическую связь между ускорениями:
Совместное решение этих трех уравнений дает возможность найти ускорения  и  также силу 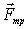 .
Выведем уравнение для кинетической энергии твердого тела при плоском движении. Пусть тело совершает плоское движение в некоторой инерциальной K-системе отсчета. Чтобы найти его кинетическую энергию Т в этой системе, воспользуемся формулой (5.12). Входящая в эту формулу величина 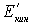 в данном случае представляет собой кинетическую энергию вращения тела в С-системе вокруг оси, проходящей через центр масс тела. Согласно (6.31)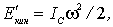 поэтому сразу можно записать
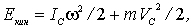 | (6.35) |
где 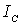 - момент инерции тела относительно оси вращения, проходящей через его центр масс, 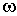 -угловая скорость тела, т - его масса, 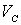 - скорость центра инерции тела в K-системе отсчета
Таким образом, кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в С-системе и энергии, связанной с движением центра масс.
3) Вращение твердого тела вокруг свободных осей.
Рассмотрим понятие свободных осей твердого тела и его главных осей инерции. Если твердое тело привести во вращение и затем предоставить самому себе, то направление оси вращения в пространстве, вообще говоря, будет меняться. Для того чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ней необходимо приложить определенные силы.
Рассмотрим этот вопрос более подробно на следующем примере. Пусть середина С однородного стержня жестко скреплена с осью вращения так, что угол между стержнем и осью равен 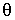 (рис. 6.19). Найдем момент 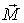 | Рис. 6.19.
Определение свободных осей твердого тела |
внешних сил, которые необходимо приложить к оси вращения, чтобы при вращении стержня с угловой скоростью 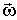 ее направление не менялось. Согласно (6.12), этот момент 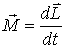 . Таким образом, чтобы определить 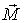 , сначала надо найти момент импульса стержня  , а затем его производную по времени.
Момент импульса  проще всего определить относительно точки С. Мысленно выделим элемент стержня массы dm, находящийся на расстоянии r от точки С. Его момент импульса относительно этой точки 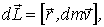 где  скорость элемента. Легко видеть, чти вектор 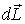 , направлен перпендикулярно стержню (рис.6.19), причем его направление не зависит от выбора элемента dm. Поэтому суммарный момент импульса 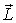 стержня совпадает по направлению с вектором 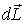 .
Заметим, что в данном случае вектор 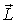 не совпадает по направлению с вектором 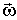 .
При вращении стержня вектор  будет также вращаться с угловой скоростью  . За промежуток времени dt вектор 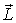 получает приращение 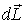 , модуль которого, как видно из рис. 6.19, равен 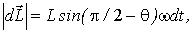 или в векторном виде 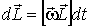 . Поделив обе части последнего выражения на dt, получим
Таким образом, действительно, для удержания оси вращения в неизменном направлении к ней необходимо в данном случае приложить момент 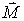 некоторых внешних сил 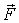 , показанных на рис. 6.19. Однако нетрудно видеть, что если 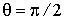 , то вектор  совпадает по направлению с вектором 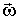 , и в этом случае  , т. е. направление оси вращения будет оставаться неизменным без внешнего воздействия.
Ось вращения, направление которой в пространстве остается неизменным без действия на нее каких-либо сил извне, называют свободной осью тела.
В общей теории доказывается, что для любого твердого тела существуют три взаимно перпендикулярные проходящие через центр инерции тела оси, которые могут служить свободными осями. Их называют главными осями инерции тела.
Нахождение главных осей инерции для тела произвольной формы - в математическом отношении сложная задача. Однако она очень упрощается для тел, обладающих той или иной симметрией, ибо положение центра инерции и направление главных осей инерции обладают в этом случае той же симметрией.
Например, у однородного прямоугольного параллелепипеда главные оси инерции проходят через центры противолежащих граней. Если тело обладает осью симметрии, как например, однородный цилиндр, одной из его главных осей инерции является ось симметрии, в качестве же остальных осей могут служить две любые взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной оси симметрии и проходящей через центр инерции тела. Таким образом, у тела с осевой симметрией фиксирована только одна из главных осей инерции. У тела с центральной симметрией (например, у однородного шара) главными осями инерции являются три любые взаимно перпендикулярные оси, проходящие через центр тела,-ни одна из главных осей инерции не фиксирована относительно тела.
Важной особенностью главных осей инерции тела является то обстоятельство, что при вращении тела вокруг любой из них момент импульса 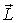 тела совпадает по направлению с угловой скоростью 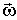 тела и определяется формулой
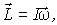 | (6.36) |
где I - момент инерции тела относительно данной главной оси инерции. Причем 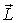 не зависит от выбора точки, относительно которой его определяют - при условии, что ось вращения неподвижна.
Наиболее просто убедиться в справедливости (6.36) можно для случая однородного тела с осевой симметрией. Действительно, согласно (6.27), момент импульса твердого тела относительно оси вращения 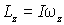 Напомним, что 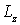 - это проекция вектора  , определенного относительно любой точки на этой оси. Но если тело симметрично относительно оси вращения, то из соображения симметрии сразу следует, что вектор 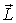 совпадает по направлению с вектором  и, значит, 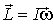 .
4) Движение твердого тела с одной неподвижной точкой.
Заметим, что в общем случае, когда ось вращения не совпадает ни с одной из главных осей инерции, хотя и проходит через центр инерции тела, направление вектора  не совпадает с вектором 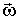 и связь между этими векторами носит сложный характер. Эго обстоятельство является причиной сложного поведения вращающихся твердых тел.
В качестве практически важного примера вращения твердого тела рассмотрим гироскопы. Гироскопом называют массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси | Рис. 6.20.
Гироскоп как пример вращения твердого тела |
симметрии. Рассмотрим поведение гироскопа на примере волчка. Опыт показывает, что если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионное движение ( прецессию) - его ось описывает конус вокруг вертикали с некоторой угловой скоростью  , причем оказывается: чем больше угловая скорость 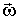 вращения волчка, тем меньше угловая скорость прецессии 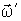 .
Такое поведение волчка гироскопа можно легко объяснить с помощью уравнения моментов (6.12), если только принять, что 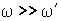 . Это условие, кстати, поясняет, что имеется в виду под большой угловой скоростью гироскопа. Действительно, момент импульса 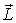 прецессирующего волчка относительно точки опоры О (рис. 6.20) можно представить в виде суммы момента импульса 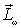 , обусловленного вращением волчка вокруг своей оси, и некоторого добавочного момента импульса 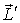 , вызванного прецессией волчка вокруг вертикальной оси, т. е.
Поскольку ось волчка совпадает с одной из главных осей инерции, то, согласно (6.36), 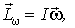 где  момент инерции волчка относительно этой оси. Кроме того, ясно, что чем меньше угловая скорость прецессии, тем меньше и соответствующий момент 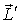 . При 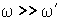 во всех практически интересных случаях  , поэтому результирующий момент импульса 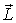 практически совпадает с 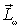 как по величине, так и по направлению, - можно считать, что
Зная же поведение вектора  , можно определить и характер движения оси волчка-гироскопа.
Поведением вектора 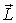 управляет уравнение моментов (6.12). Согласно ему, момент импульса 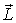 относительно точки O (рис. 6.20) получает за время dt приращение
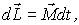 | (6.37) |
совпадающее пo направлению с вектором  - моментом внешних сил относительно той же точки О. В данном случае это момент силы тяжести 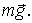 Из рис.6.20 видно, что 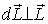 . В результате вектор 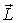 , а следовательно, и ось волчка, будет поворачиваться вместе с вектором 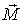 вокруг вертикали, описывая круговой конус с углом полураствора 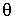 . Волчок-гироскоп будет прецессировать вокруг вертикальной оси с некоторой угловой скоростью.
Найдем связь между векторами 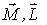 и  . Согласно рисунку, модуль приращения вектора 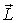 за время dt есть  , или в векторном виде 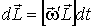 . После подстановки этого выражения в (6.37) получим
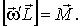 | (6.38) |
Из этого уравнения видно, что момент силы  определяет угловую скорость прецессии 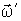 , а не ускорение. Поэтому мгновенное устранение момента 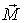 приводит к мгновенному исчезновению и прецессии. В этом отношении можно сказать, что прецессия не обладает инерцией.
Заметим, что момент сил 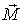 , действующий на гироскоп, может иметь любую природу. Для обеспечения постоянной угловой скорости прецессии 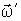 важно только, чтобы вектор 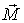 , не меняясь по модулю, поворачивался вместе с осью гироскопа.
Пример. Найти угловую скорость прецессии наклонного волчка массы т, вращающегося с большой угловой скоростью 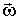 вокруг своей оси симметрии, относительно которой момент инерции волчка равен I. Центр масс волчка находится на расстоянии l от точки опоры.
Согласно (6.38), 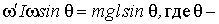 угол между вертикалью и осью волчка (рис. 6.20). Отсюда
Интересно, что величина 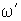 не зависит от угла наклона  оси волчка. Кроме того, полученный результат показывает, что угловая скорость прецессии  обратно пропорциональна 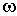 , т. е., действительно, чем больше угловая скорость волчка, тем меньше угловая скорость его прецессии.
В конце параграфа введем понятие гироскопического момента сил. Для этого рассмотрим эффект, возникающий при вынужденном вращении оси гироскопа. Пусть, например, ось гироскопа укреплена в U-образной подставке, которую мы будем поворачивать вокруг оси 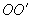 как показано на рис. 6.21. Если момент импульса гироскопа  направлен вправо, то при | Рис. 6.21.
Гироскопический момент сил |
таком повороте за время dt вектор  получит приращение  - вектор, направленный за плоскость рисунка. Согласно (6.37), это означает, что на гироскоп действует момент сил 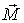 , совпадающий по направлению с вектором 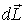 . Момент 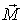 обусловлен возникновением пары сил F, действующих на ось гироскопа со стороны подставки. Ось же гироскопа в соответствии с третьим законом Ньютона будет действовать на подставку с силами F' (рис. 6.21). Эти силы называют гироскопическими они создают гироскопический момент . Заметим, что в данном случае гироскоп не обладает способностью противодействовать изменению направления его оси вращения.
Появление гироскопических сил называют гироскопическим эффектом. Подобный гироскопический эффект, связанный с возникновением гироскопического давления на подшипники, наблюдается, например, у роторов турбин на кораблях при поворотах и качке, у винтовых самолетов при виражах и т.п.
Проследим действие гироскопического момента на примере гироскопа, ось которого вместе с рамкой (рис. 6.22) может свободно поворачиваться вокруг горизонтальной оси 00' U-образной подставки. | Рис. 6.22.
Пример гироскопа с подвижной осью |
Если подставке сообщить вынужденное вращение вокруг вертикальной оси, как показано на рисунке вектором  , то момент импульса 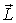 гироскопа получит за время dt приращение 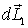 - вектор, направленный за рисунок. Эго приращение обусловлено моментом 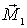 пары сил, действующих на ось гироскопа со стороны рамки. Гироскопические силы, действующие со стороны оси гироскопа на рамку, вызовут поворот последней вокруг горизонтальной оси 00'. При этом вектор 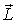 получит дополнительное приращение 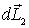 которое в свою очередь обусловлено моментом 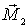 пары сил, действующих на ось гироскопа со стороны рамки. В результате ось гироскопа будет поворачиваться так, что вектор 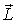 будет стремиться совпасть по направлению с вектором 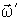 .
Таким образом, за время dt момент импульса гироскопа 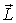 получает приращение 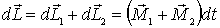 . При этом на рамку действует гироскопический момент
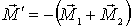 .
Составляющая этого момента  вызывает поворот рамки вокруг горизонтальной оси 00', другая составляющая 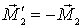 противодействует противодействует повороту всей системы вокруг вертикальной оси (в отличие от предыдущего случая).
Гироскопический эффект лежит в основе разнообразных применений гироскопов: гирокомпас, гироскопический успокоитель качки кораблей, гироскопический стабилизатор и др.
|