4.2. Импульс. Закон его сохранения
Импульс частицы - это произведение ее массы на скорость 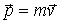 . Другое название этой величины - количество движения. Опыт и соответствующий анализ механических явлений показывают, что механическое движение тел характеризуется двумя величинами, которые являются основными мерами механического движения тел: первая - скалярная, вторая - векторная. Это кинетическая энергия 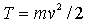 и импульс частицы 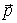 .Обе они играют центральную роль во всем построении механики.
Перейдем к более подробному рассмотрению импульса. Прежде всего, запишем основное уравнение ньютоновой динамики (3.6) в иной форме-через импульс:
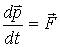 | (4.1) |
т. е. производная импульса материальной точки по времени равна действующей на нее силе. В частности, если  . то 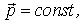 то есть при такой записи видна четкая логическая связь между 1 и 2 законами Ньютона : первый закон утверждает, что импульс является сохраняющейся в отсутствии взаимодействия мерой движения, а второй описывает ее изменение при наличии взаимодействия.
Заметим, что в неинерциальной системе отсчета результирующая сила 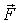 включает в себя не только силы взаимодействия данной частицы с другими телами, но и силы инерции.
Уравнение (4.1) позволяет найти приращение импульса частицы за любой промежуток времени, если известна зависимость силы 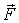 от времени. Действительно, из (4.1) следует, что элементарное приращение импульса частицы за промежуток времени 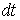 есть 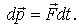 Последняя величина называется импульсом силы. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени 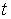 :
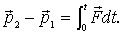 | (4.2) |
Если сила 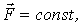 то вектор 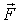 можно вынести из-под интеграла и тогда 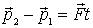 . Таким образом, приращение импульса частицы за любой промежуток времени равно импульсу действующей на нее силы за то же время.
Пример. На частицу, которая в начальный момент 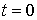 имела импульс | Рис. 4.1.
Определение приращения импульса |
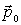 , действует в течение промежутка времени 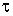 сила 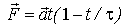 , где 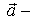 постоянный вектор. Найти, импульс 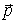 частицы после окончания действия этой силы. Согласно (4.2), получим 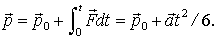
Перейдем к рассмотрению более сложного случая. Рассмотрим произвольную систему частиц. Введем понятие импульса системы как векторной суммы импульсов ее отдельных частиц:
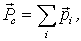 | (4.3) |
где 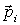 - импульс 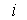 частицы. Заметим, что импульс системы 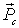 - величина аддитивная, т. е. импульс системы равен сумме импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
Найдем физическую величину, которая определяет изменение импульса системы. Для этого продифференцируем соотношение (4.3) по времени:
где 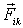 - силы, действующие на 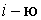 частицу со стороны других частиц системы, которые обычно называют внутренние силы; 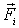 - сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему, т.е. равнодействующая внешних сил. Подставив последнее выражение в предыдущее, получим
В этом равенстве двойная сумма справа - это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению. Поэтому результирующая сила в каждой паре взаимодействия равна нулю, а значит, равна нулю и векторная сумма всех внутренних сил. В результате последнее уравнение принимает следующий вид:
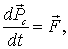 | (4.4) |
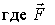 - результирующая всех внешних сил 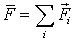 .
Уравнение (4.4) означает: производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на частицы системы.
Как и в случае одной частицы, из уравнения (4.4) следует, что приращение импульса системы за конечный промежуток времени 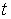 есть
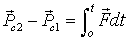 | (4.5) |
т. е. приращение импульса системы равно импульсу результирующей всех внешних сил за соответствующий промежуток времени. В соотношении (4.5), конечно, 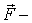 результирующая всех внешних сил, действующих на тела системы.
Уравнения (4.4) и (4.5) справедливы как в инерциальной, так и в неинерциальной системах отсчета, если в неинерциальной системе отсчета учесть и действие сил инерции, играющих роль внешних сил, т. е. под 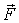 в этих уравнениях надо понимать сумму 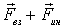 , где результирующая всех внешних сил взаимодействия - это 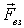 , а результирующая всех сил инерции обозначена  .
Из уравнения (4.4) можно сделать важный вывод - импульс системы может изменяться под действием только внешних сил. Внутренние силы не могут изменить импульс системы независимо от их конкретного вида. Система, на которую не действуют внешние силы, называется замкнутой. Отсюда непосредственно вытекает и другой важный вывод - закон сохранения им пульса: в инерциальной системе отсчета импульс замкнутой системы частиц остается постоянным, т. е. не меняется со временем:
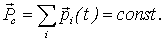 | (4.6) |
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем, что и подчеркнуто в последнем выражении. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Другими словами, отдельные части замкнутой системы могут только обмениваться импульсами. Обнаружив в некоторой системе приращение импульса, можно утверждать, что это. приращение произошло за счет убыли импульса в окружающих телах.
В этом смысле уравнение (4.4) и. (4.5) следует рассматривать как более общую формулировку закона изменения импульса, формулировку, в которой указана причина изменения импульса у незамкнутой системы - действие других тел, то есть внешних сил. Сказанное справедливо, разумеется, только по отношению к инерциальным системам отсчета.
Импульс может сохраняться и у незамкнутой системы при условии, что результирующая всех внешних сил равна нулю. Это непосредственно вытекает из уравнений (4.4) и (4.5). В практическом отношении сохранение импульса в этих случаях представляет особый интерес, ибо дает возможность получать достаточно простым путем ряд заключений о поведении системы, не вникая в детальное рассмотрение процесса.
Кроме того, у незамкнутой системы может сохраняться не сам импульс  , а его проекция 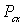 на некоторое направление 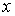 . Это бывает тогда, когда проекция результирующей внешней силы 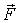 на направление 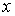 равна нулю, т. е. вектор 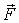 перпендикулярен ему. Действительно, спроектировав уравнение (4.4), получим
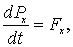 | (4.7) |
откуда следует, что если 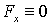 , то 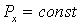 . Например, при движении системы в однородном поле сил тяжести сохраняется проекция ее импульса на любое горизонтальное направление, при любых внутренних процессах в системе.
Рассмотрим ряд примеров на изменение и сохранение импульса.
Пример 1. Орудие массы 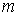 соскальзывает по гладкой наклонной плоскости, составляющей угол 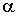 с горизонтом. В момент, когда скорость орудия равна 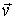 , произвели выстрел, в результате которого орудие остановилось, а вылетевший в горизонтальном направлении снаряд "унес" импульс р. Пусть продолжительность выстрела равна 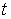 . Каково среднее за время 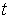 значение силы реакции 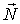 со стороны наклонной плоскости?
Здесь система орудие - снаряд незамкнутая. За время 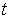 эта система получает приращение импульса, равное 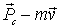 . Изменение импульса системы обусловлено действием двух внешних сил: силы реакции 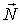 (она перпендикулярна наклонной плоскости) и силы тяжести 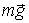 . Поэтому можно написать:
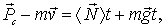 ,
где 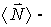 среднее за время t значение вектора 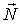 . Это соотношение очень | Рис. 4.2.
Диаграмма изменения импульса |
полезно представить графически (рис. 4.2). Из рисунка сразу видно, что искомое среднее значение величины 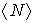 определяется формулой
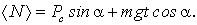 .
Пример 2. На поверхности озера покоится узкий плот массы 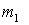 с человеком масс 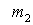 . Человек совершил перемещение 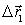 относительно плота и затем остановился. Сопротивление воды пренебрежимо мало. Найдем соответствующее перемещение плота 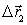 относительно берега.
В данном случае результирующая всех внешних сил, действующих на систему человек - плот, равна нулю, а поэтому импульс этой системы меняться не будет, оставаясь равным нулю в процессе движения:
где 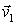 и 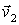 - скорости плота и человека относительно берега. Но скорость человека относительно берега можно представить в виде 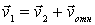 , где 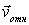 - скорость человека относительно плота. Исключив 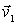 из этих двух уравнений, получим
Умножив обе части на 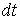 , найдем связь между элементарными перемещениями плота 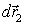 и человека 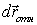 . относительно плота. Такая же связь будет, очевидно, и для конечных перемещений:
Отсюда видно, что результирующее перемещение плота 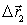 не зависит от характера движения человека, т. е. не зависит от закона 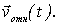
Подчеркнем еще раз: закон сохранения импульса выполняется только в инерциальных системах. Это, однако, не исключает случаев, когда импульс системы сохранялся бы и в неинерциальных системах отсчета. Для этого достаточно, чтобы в уравнении (4.4), справедливом и в неинерциальных системах отсчета, внешняя сила 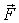 , которая включает в себя и силы инерции, была равна нулю. Ясно, что такое положение может осуществляться лишь при специальных условиях, которые встречаются довольно редко и имеют частный характер.
Докажем, что если импульс системы сохраняется в одной инерциальной системе отсчета 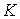 , то он сохраняется и в любой другой инерциальной системе 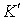 . Пусть в системе 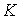
Если система 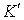 движется относительно системы  со скоростью 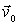 , то скорость 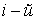 частицы в системе 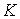 можно представить как 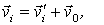 где 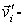 скорость этой частицы в системе 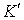 . Тогда выражение для импульса системы можно преобразовать к следующему виду 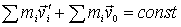 . Вторая сумма в этом равенстве не зависит oт времени. А это значит, что и первая сумма - импульс системы в системе отсчета 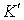 - тоже не зависит от времени, т. е.
Полученный результат полностью соответствует принципу относительности Галилея, согласно которому законы механики одинаковы во всех инерциальных системах отсчета.
Приведенный вывод закона сохранения импульса опирался только на справедливость законов Ньютона. В частности, предполагалось, что частицы замкнутой системы взаимодействуют между собой попарно и это взаимодействие подчиняется третьему закону Ньютона. А как обстоит дело в случае систем, не подчиняющихся законам Ньютона, например, в системах с электромагнитным излучением?
Ответ на этот вопрос дает опыт, который со всей убедительностью показывает, что закон сохранения импульса оказывается справедливым и для таких систем. Однако в этих случаях в общем балансе импульса необходимо учитывать не только импульсы частиц, но и импульс, которым обладает, как выясняется в электродинамике, само поле излучения. Примером экспериментального проявления существования импульса у электромагнитного излучения служит давление, оказываемое светом на твердые тела и газы, что впервые было показано в опытах П.Н. Лебедева, выполненных в первое десятилетие ХХ века.
Таким образом, опыт показывает, что закон сохранения импульса, надлежащим образом обобщенный, представляет собой фундаментальный закон природы, не знающий никаких исключений. Но в таком широком понимании он уже не является следствием законов Ньютона, а должен рассматриваться как самостоятельный общий принцип, являющийся обобщением опытных фактов. О связи закона сохранения импульса со свойством однородности пространства будет сказано далее.
|