3.5. Решение основной задачи динамики
Основное уравнение динамики частицы представляет собой не что иное, как математическое выражение второго закона Ньютона:
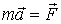 . . | (3.14) |
Уравнение (3.14) это дифференциальное уравнение движения частицы в векторном виде. Его решение - основная задача динамики материальной точки. При этом возможны две различные постановки задачи.
1. Найти действующую на частицу 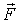 , если известны масса m точки и зависимость от времени ее радиус-вектора 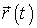 .
2. Найти закон движения частицы, т. е. зависимость от времени ее радиус-вектора 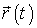 , если известны масса т частицы, действующая на нее сила 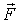 (или силы 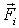 ) и начальные условия - скорость 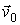 и положение 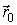 частицы в начальный момент времени.
В первом случае задача сводится к дифференцированию 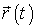 по времени, во втором - к интегрированию уравнения (3.14). Математическая сторона этого вопроса достаточно подробно была рассмотрена в предшествующем разделе о кинематике точки.
В зависимости от характера и постановки конкретной задачи решение уравнения (3.14) проводят одним из трех способов: в векторной форме, в координатах или в проекциях на касательную и нормаль к траектории в данной точке. Рассмотрим вид уравнения (3.14) в последних двух случаях.
В проекциях на оси декартовых координат. Проектируя обе части уравнения (3.14) на оси х, у, z, получим три дифференциальных уравнения вида
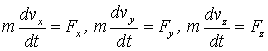 , , | (3.15) |
где 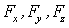 - проекции вектора 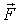 на оси х, у, z. Необходимо помнить, что эти проекции - величины алгебраические, т.е. в зависимости от ориентации вектора 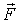 они могут быть как положительными, так и отрицательными. Знак проекции результирующей силы 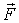 определяет и знак проекции вектора ускорения.
Рассмотрим на конкретном примере, в чем заключается стандартный подход к решению задач с помощью уравнений (3.15). Небольшой брусок массы т скользит вниз по наклонной плоскости, составляющей угол 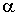 с горизонтом. Коэффициент трения равен 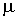 . Необходимо определить ускорение бруска относительно плоскости, которая может рассматриваться как инерциальная система отсчета.
На первом этапе решения следует изобразить все силы, действующие на брусок. Это сила тяжести 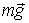 , нормальная сила реакции 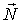 со стороны плоскости и сила трения 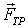 (рис. 3.2), направленная в сторону, | Рис. 3.2.
Скольжение частицы по наклонной плоскости |
противоположную движению бруска. Систему координат x, у, z свяжем с с неподвижной наклонной плоскостью, как показано на рисунке. В любой задаче систему координат можно ориентировать произвольно, но во многих случаях (и, в частности, на рис. 3.2) выбор направления осей задается характером движения. В данном случае заранее известно возможное направление движения бруска, поэтому наиболее целесообразно оси координат расположить так, чтобы одна из них совпадала с направлением движения. Тогда задача сведется к решению только одного уравнения (3.15).
Следует заметить, что таким выбором мы учли влияние на движение ограничений (связей), налагаемых плоскостью, которую полагаем жесткой конструкцией неизменной формы. Развитием этой идеи по учету влияния связей на движение тела является введение обобщенных координат и конфигурационного пространства, где поведение системы описывается с помощью функции Лагранжа. Такой подход обычно изучается в курсе теоретической механики.
Выберем ось х, как показано на рис. 3.2, обязательно указав при этом ее положительное направление (стрелкой). Теперь можно приступить к составлению уравнений (3.15): слева - произведение массы т бруска на проекцию его ускорения ax и справа - проекции всех сил па ось x:
В данном случае 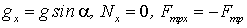 , следовательно
Так как тело движется только вдоль оси х, то это значит, согласно второму закону Ньютона, что сумма проекций всех сил на любое перпендикулярное оси х направление равна нулю. Выбрав в качестве такого направления ось у (рис. 3.2), c учетом закона Кулона-Амонтона, связывающего силу трения и нормальной реакции, получим при условии, что началось скольжение тела
В итоге 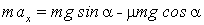 . Если правая часть этого уравнения окажется положительной, то и 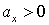 , а это значит, что 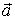 направлен вниз по наклонной плоскости. Если же наоборот, то это значит, что сделанное предположение о начале скольжения неверно, и тело будет удерживаться силой трения в покое на наклонной плоскости.
В проекциях на касательную и нормаль к траекторий в данной точке. Проектируя обе части (3.15) на подвижные векторы нормали к траектории 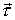
и 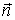 (рис. 3.3) и используя полученные ранее выражения для тангенциального и нормального ускорений, запишем:
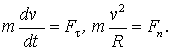 | (3.16) |
где 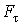 и 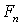 - проекции вектора 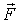 на орты 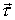 н 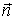 . На рис. 3.3. обе проекции положительные. Векторы 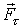 и 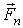 называют тангенциальной и нормальной составляющими силы 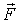 . Напомним, что направление орта 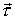 выбирают в | Рис. 3.3.
Разложение сил на подвижные орты |
сторону возрастания дуговой координаты, а направление орта 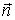 - к центру кривизны траектории в данной точке. Уравнениями (3.16.) удобно пользоваться, если заранее известна траектория материальной точки.
Рассмотрим пример их применения. Пусть небольшое тело А начинает соскальзывать с вершины гладкой сферы радиуса r. Определим скорость тела в момент отрыва от поверхности сферы. Изобразим силы, действующие на тело А (это сила тяжести 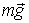 , и нормальная сила реакции 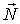 ), и запишем уравнения (3.10) в проекциях на направления векторов 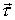 н 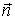 (рис. 3.4).
| Рис. 3.4.
Соскальзывание частицы с полусферы |
здесь индекс ? несуществен, поэтому он опущен. Преобразуем первое уравнение к виду, удобному для интегрирования. Воспользовавшись тем, что 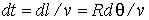 , где 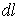 - элементарный путь тела А за промежуток времени 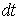 , перепишем первое уравнение в виде 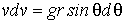 . Проинтегрируем левую часть этого выражения от 0 до v, правую- от 0 до 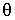 , и получим
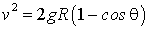 .
При отрыве тела от поверхности 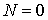 , поэтому второе исходное уравнение принимает вид 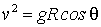 , где v и ?' соответствуют точке отрыва. Исключив 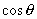 из последних двух равенств, получим 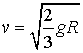 .
|