4.5. Краткое введение в термодинамику необратимых процессов
Применение законов равновесной термодинамики ограничено случаем, когда температура 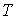 , давление 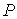 и другие параметры состояния во всех точках системы одинаковы. Если это не так, то в термодинамической системе возникают необратимые процессы. Для описания необратимых процессов можно воспользоваться гипотезой локального равновесия, заключающейся в предположении, что внутри малого объема среды выполняется основное уравнение термодинамики равновесных процессов. Если в качестве параметров состояния ввести локальную плотность внутренней энергии 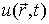 , приходящуюся на единицу массы среды, и удельный объем  , то для точки среды с координатами 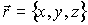 в момент времени 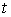 можно записать уравнение 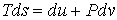 , , | (4.73) |
где:  - локальная плотность энтропии на единицу массы среды, 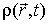 - локальная плотность среды. Тогда внутренняя энергия 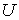 всей системы определяется с помощью выражения 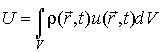 , , | (4.74) |
а ее энтропия 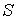 соответственно может быть найдена по формуле 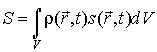 . . | (4.75) |
Совместное применение уравнения (4.73) с уравнениями баланса массы, внутренней энергии и других термодинамических величин, позволяет построить феноменологическую термодинамику необратимых процессов. Ключевое значение в неравновесной термодинамике имеет величина, численно равная скорости увеличения энтропии в единице объема:
 . . | (4.76) |
Эта величина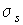 представляет собой производство энтропии для единичного объема адиабатически изолированной системы. представляет собой производство энтропии для единичного объема адиабатически изолированной системы. Если в качестве термодинамических параметров системы выступают 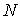 величин 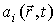 , то формулу (4.76) можно представить в виде: 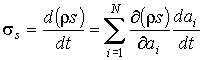 . . | (4.77) |
Величины  называются термодинамическими силами, а величины  - плотностями термодинамических потоков. Следовательно, производство энтропии 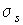 можно определить по формуле: 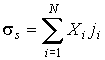 . . | (4.78) |
В случае небольших отклонений от равновесного состояния между термодинамическими потоками 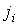 и термодинамическими силами 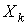 может быть установлена линейная зависимость  . . | (4.79) |
Это соответствует наиболее простому случаю линейной термодинамики.
Таким образом, для линейной термодинамики производство энтропии определяется выражением
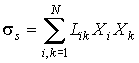 | (4.80) |
или
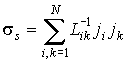 . . | (4.81) |
Коэффициенты  называются кинетическими коэффициентами, и они характеризуют интенсивность явлений переноса. называются кинетическими коэффициентами, и они характеризуют интенсивность явлений переноса. В 1931 году американский физик и химик Ларс Онсагер (1903 - 1976) установил, что для кинетических коэффициентов выполняется условие:
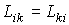 , , | (4.82) |
указывающее на симметрию матрицы кинетических коэффициентов. Выражение (4.82) называется соотношением взаимности Онсагера. Одним из принципов линейной неравновесной термодинамики является предложенный в 1947 году бельгийским физико-химиком Ильей Романовичем Пригожиным (р. 1917) принцип минимума производства энтропии:
Стационарные необратимые процессы протекают таким образом, чтобы производство энтропии было минимальным.
Принцип Пригожина позволяет установить какие процессы реализуются в природе, а какие нет, и, таким образом, выбрать из возможных процессов реально существующие.
Необходимость выполнения указанного принципа приводит к тому, что при протекании в среде необратимых стационарных процессов возникают динамические структуры, названные Пригожиным диссипативными структурами, что уменьшает производство энтропии. Примером таких структур могут служить ячейки Бенара - регулярные динамические структуры, возникающие в тонком слое нагреваемой снизу жидкости, и колебательные химические реакции Б.П. Белоусова, при которых происходят периодические изменения концентрации реагирующих веществ.
|