| |
 |
3.3. Расчет цикла Карно для реального газа
Проведем расчет к.п.д. цикла Карно для реального газа, уравнение состояния которого является уравнением достаточно произвольного вида
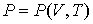 , , | (3.14) |
а внутренняя энергия задается формулой
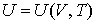 . . | (3.15) |
Необходимо отметить, что феноменологическая термодинамика не дает возможности теоретически получить вид этих функций, а для их построения требуется использование экспериментальных данных или результатов статистической физики.
Для рассматриваемого случая реального газа можно получить уравнение адиабаты. Подстановка формул (3.14) и (3.15) уравнение для адиабатического процесса: 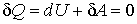 , позволяет получить дифференциальное уравнение 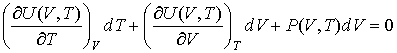 , , | (3.16) |
интегрирование которого дает уравнения адиабат для процессов 2-3 и 4-1 (см. рис. 3.5) в виде:
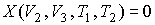 , , | (3.17) |
 . . | (3.18) |
Уравнения (3.17) и (3.18) могут быть разрешены в явном виде относительно переменных 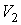 и 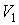 :  , , | (3.19) |
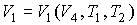 , , | (3.20) |
или относительно переменных 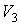 и 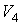 : 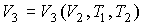 , , | (3.21) |
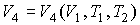 . . | (3.22) |
Для изотермических процессов 1-2 и 3-4 запишем общие выражения для получаемой 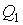 и отдаваемой 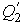 теплоты: 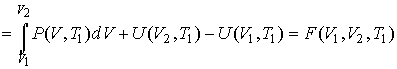 , , | (3.23) |
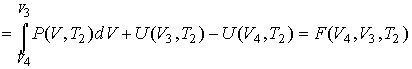 . . | (3.24) |
В этих формулах учтено то, что для реального газа при изотермическом процессе может происходить изменение внутренней энергии.
Тогда в соответствии с формулой (3.2) имеем выражение для к.п.д. цикла Карно  . . | (3.25) |
Подставляя в эту формулу выражения для 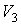 и 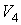 из уравнений (3.21) и (3.22) имеем 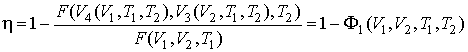 . . | (3.26) |
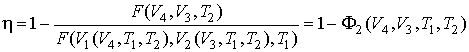 . . | (3.27) |
 , , | (3.28) |
которое может выполняться при произвольных значениях 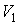 , 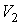 , 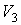 и 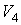 только в том случае, если функции 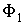 и  представляют собой одинаковые зависимости от температур 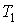 и 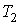 и не зависят соответственно от 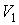 , 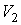 и 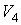 , 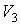 . Следовательно, к.п.д. цикла Карно тепловой машины для рассмотренного случая является функцией температуры нагревателя 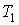 и холодильника  и может быть записан в виде 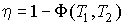 . . | (3.29) |
Отметим, что проведенный анализ не позволяет сделать заключение о зависимости или независимости конкретного вида этой функции от физических свойств рабочего тела.
Задача 3.2. Рассчитать к.п.д. термодинамического цикла Карно для тепловой машины, использующей в качестве рабочего тела один моль реального газа, описываемого уравнением Ван-дер-Ваальса. Использовать уравнение состояния 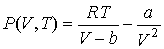 и выражение для внутренней энергии и выражение для внутренней энергии 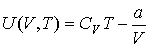 газа Ван-дер-Ваальса. газа Ван-дер-Ваальса.
Решение: Подстановка в формулу (3.16) приведенных в условии задачи выражений для уравнения состояния и внутренней энергии газа Ван-дер-Ваальса дает:
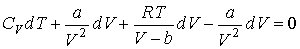 .
Полученное выражение может быть приведено к виду:
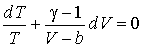 ,
где введено обозначение:
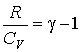 .
Интегрирование полученного дифференциального уравнения дает уравнение адиабаты газа Ван-дер-Ваальса:
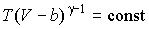 .
Применение этого уравнения для двух адиабатических процессов позволяет получить условия:
 ,
 ,
которые в свою очередь дают:
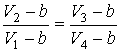 .
Далее, подстановка в формулы (3.23) и (3.24) выражений для функций 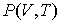 и и 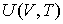 , и выполнение интегрирования позволяет вычислить подводимую , и выполнение интегрирования позволяет вычислить подводимую 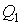 и отводимую и отводимую 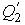 теплоты: теплоты:
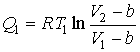 ,
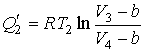 .
Подстановка этих выражений в формулу (3.2), с учетом полученного выше соотношения для объемов, дает выражение для к.п.д. машины Карно, при использовании в ней газа Ван-дер-Ваальса:
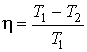 .
Нетрудно видеть, что эта формула полностью совпадает с выражением (3.13) для к.п.д. машины Карно, использующей идеальный газ.
Задача 3.3. Рассчитать к.п.д. термодинамического цикла Карно для тепловой машины, использующей в качестве рабочего тела фотонный газ. Использовать уравнение состояния 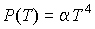 и выражение для внутренней энергии и выражение для внутренней энергии 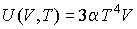 фотонного газа. Термодинамический цикл Карно для фотонного газа приведен на рис. 3.6. фотонного газа. Термодинамический цикл Карно для фотонного газа приведен на рис. 3.6. | Рис. 3.6.
Термодинамический цикл Карно для фотонного газа |
Решение: Фотонный газ представляет собой электромагнитные волны, заполняющие объем, ограниченный стенками, нагретыми до некоторой температуры 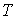 . .
Применение формулы (3.16) для приведенных в условии задачи выражений для уравнения состояния и внутренней энергии фотонного газа позволяет получить дифференциальное уравнение адиабатического процесса:
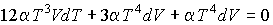 .
Данное дифференциальное уравнение преобразуем к виду:
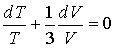 .
Интегрирование этого дифференциального уравнения позволяет записать уравнение адиабаты фотонного газа в форме:
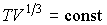 .
Тогда, применение этого уравнения для двух адиабатических процессов позволяет получить условия:
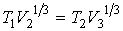 ,
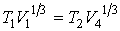 ,
из которых следует:
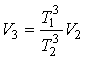 ,
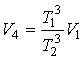 .
Подстановка в формулы (3.23) и (3.24) выражения для функций  и и 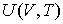 из условия задачи, и выполнение интегрирования позволяет вычислить подводимую из условия задачи, и выполнение интегрирования позволяет вычислить подводимую 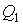 и отводимую и отводимую 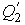 теплоты: теплоты:
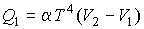 ,
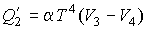 .
Тогда по формуле (3.2) имеем
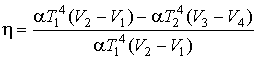 .
Учет полученных выше соотношений между объемами 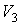 , ,  и и  , , 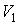 позволяет записать к.п.д. машины Карно, рабочим телом которой является фотонный газ в виде: позволяет записать к.п.д. машины Карно, рабочим телом которой является фотонный газ в виде:
 .
Как следует из проведенных расчетов к.п.д. машины Карно одинаков при использовании в ней в качестве рабочего тела идеального газа, газа Ван-дер-Ваальса и фотонного газа.
|
 |
|