|
|
|||
|
|||
|
ГЛАВА 6
6.3. Эффузия в разреженном газе |
|
В параграфе 6.2 отмечалось, что коэффициенты теплопроводности и вязкости не зависят от плотности газа. Однако постоянство этих коэффициентов сохраняется, только если плотность газа достаточно велика. Для сильно разреженного газа, плотность которого столь мала, что длина свободного пробега его молекул
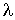 становится сравнима с характерным размером сосуда становится сравнима с характерным размером сосуда 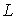 , коэффициенты теплопроводности и вязкости начинают зависеть от плотности. С уменьшением плотности газа эти коэффициенты начинают уменьшаться. Связано это с тем, что при увеличении длины свободного пробега , коэффициенты теплопроводности и вязкости начинают зависеть от плотности. С уменьшением плотности газа эти коэффициенты начинают уменьшаться. Связано это с тем, что при увеличении длины свободного пробега 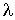 до характерного размера сосуда до характерного размера сосуда 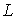 , молекулы газа начинают гораздо реже сталкиваться друг с другом и гораздо чаще со стенками сосуда. При этом обмен энергией и импульсом происходит уже не между молекулами газа, а непосредственно между стенками сосуда. , молекулы газа начинают гораздо реже сталкиваться друг с другом и гораздо чаще со стенками сосуда. При этом обмен энергией и импульсом происходит уже не между молекулами газа, а непосредственно между стенками сосуда.Состояние газа, при котором длина свободного пробега его молекул
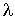 становится порядка или более характерного размера сосуда становится порядка или более характерного размера сосуда 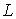 , в котором находится газ, называется вакуумом. , в котором находится газ, называется вакуумом.Различают низкий вакуум, при котором
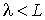 , средний, когда , средний, когда 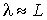 и высокий (или глубокий), при котором и высокий (или глубокий), при котором 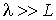 . .Отметим, что газ при одной и той же плотности в сосудах разного размера может находиться в обычном состоянии при
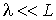 и описываться полученными выше уравнениями переноса, а может представлять собой вакуум при и описываться полученными выше уравнениями переноса, а может представлять собой вакуум при 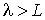 , для описания которого эти уравнения не применимы. , для описания которого эти уравнения не применимы.Рассмотрим процесс переноса в разреженном газе. Пусть имеется заполненный разреженным газом сосуд, разделенный перегородкой с небольшим отверстием. Будем считать, что размер отверстия и толщина перегородки меньше длины свободного пробега молекул газа.
Процесс истечения разреженного газа из отверстия, характерные размеры которого много меньше длины свободного пробега, называется эффузией.
Если стенки одной части сосуда поддерживать при температуре
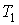 , а второй - при температуре , а второй - при температуре 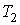 , то плотность потока молекул из первой части сосуда во вторую можно определить по формуле (6.6) , то плотность потока молекул из первой части сосуда во вторую можно определить по формуле (6.6)
а из второй в первую соответственно с помощью выражения
где:
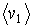 и и 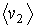 - средние скорости молекул в первой и во второй частях сосуда, зависящие от температур - средние скорости молекул в первой и во второй частях сосуда, зависящие от температур 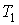 и и 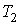 , , 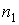 и и 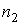 - соответственно концентрации молекул в этих частях сосуда. - соответственно концентрации молекул в этих частях сосуда.Будем считать, что молекулы, движущиеся в отверстии навстречу друг другу, не сталкиваются между собой. Тогда подстановка в эти формулы выражения (6.18) для средней скорости молекул и зависимости концентрации молекул
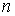 от давления от давления 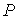 и температуры и температуры 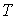 для идеального газа (см. формулу (2.32)), позволяет определить суммарную плотность потока для идеального газа (см. формулу (2.32)), позволяет определить суммарную плотность потока 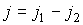 из первой части сосуда во вторую из первой части сосуда во вторую
где:
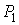 и и 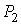 - давления газа в первой и во второй частях сосуда соответственно. - давления газа в первой и во второй частях сосуда соответственно.Формула (6.35) описывает процесс эффузии разреженного газа через маленькое отверстие в перегородке между двумя частями сосуда, газ в которых имеет соответственно температуры
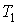 и и 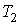 и давления и давления 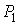 и и 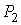 . Эта формула является приближенной, справедливой с точностью до постоянного множителя порядка единицы. . Эта формула является приближенной, справедливой с точностью до постоянного множителя порядка единицы.Выражение (6.35) позволяет получить условие, при котором разреженный газ в двух частях сосуда будет находиться в равновесии. Полагая в формуле (6.35) плотность потока
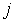 равной нулю: равной нулю: 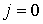 , имеем , имеем
Из формулы (6.36) следует, что если температуры стенок в двух частях рассматриваемого сосуда различны, то в состоянии равновесия давление разреженного газа в этих частях будет так же различным. В части сосуда с большей температурой стенок давление газа так же будет большим.
Условие равновесия разреженного газа (6.36) существенно отличается от аналогичного условия для не разреженного газа, длина свободного пробега молекул которого много меньше характерного размера отверстия в перегородке сосуда. Для такого газа, как известно, равновесие наступает при равенстве давлений в обеих частях сосуда.
Одним из следствий выражения (6.36) является то, что если давления
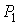 и и 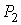 были первоначально одинаковыми, то вследствие эффузии газ начнет перетекать из области с более низкой температурой, в область с более высокой. Это явление называется тепловой эффузией. были первоначально одинаковыми, то вследствие эффузии газ начнет перетекать из области с более низкой температурой, в область с более высокой. Это явление называется тепловой эффузией. Для разделения газовых смесей, в частности смесей изотопов, нашло применение явление изотермической диффузии. Это явление заключается в том, что газ из смеси, молекулы которого легче, более интенсивно проходит через пористую перегородку, чем газ, имеющий более тяжелые молекулы. Изотермическая диффузия нашла применение, в частности, для разделения изотопов урана при его обогащении.
В разреженном газе имеет место радиометрический эффект - отталкивание от нагретой поверхности (пластины) другой, более холодной пластины. Если длина свободного пробега молекул газа сравнима или меньше расстояния между пластинами, то происходит непосредственный перенос импульса молекулами газа от горячей пластины к холодной, что и приводит к появлению силы отталкивания.
При высоком вакууме сила отталкивания пропорциональна давлению газа, а при низком - обратно пропорциональна этому давлению. Указанная особенность объясняется тем, что при длине свободного пробега, превышающей расстояние между пластинами, переносимый импульс пропорционален количеству молекул, сталкивающихся с пластинами. При более высоких давлениях, когда длина свободного пробега становится меньше расстояния между пластинами, молекулы, летящие от нагретой пластины, теряют часть своей кинетической энергии при столкновениях с другими молекулами газа. Это приводит к уменьшению силы отталкивания с ростом концентрации молекул.
Технической реализацией радиометрического эффекта являются радиометрические манометры - приборы, в которых одна из пластин является подвижной и по её смещению можно, зная зависимость силы отталкивания от давления, измерить давление разреженного газа. Обычно считают, что оно пропорционально силе отталкивания.
Область применения радиационных манометров со стороны высоких давлений (низкий вакуум с давлением газа порядка обычно 102 - 103 Па) определяется сравнимостью длины свободного пробега с расстоянием между пластинами, а со стороны низких давлений (высокий вакуум с давлением 10-3 - 10-2 Па) - проявлением давления инфракрасного излучения со стороны нагретой пластины.
|
|
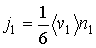 ,
,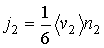 ,
,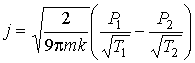 ,
,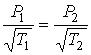 .
.