|
|
|||
|
|||
|
ГЛАВА 2
2.1. Уравнение состояния идеального газа |
|
Уравнение состояния термодинамической системы представляет собой аналитическую формулу, связывающую параметры состояния системы. Если состояние системы может быть полностью описано с помощью трех параметров: давления
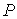 , объема , объема 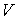 и температуры и температуры 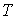 , то уравнение состояния в самом общем виде будет иметь форму: , то уравнение состояния в самом общем виде будет иметь форму:
Конкретный вид этой формулы зависит от физических свойств рассматриваемой термодинамической системы.
Обобщение многочисленных экспериментальных данных показывает, что большинство газов при комнатной температуре и давлении порядка одной атмосферы (при нормальных условиях) с достаточно высокой точностью могут быть описаны уравнением состояния, называемым уравнением Клапейрона-Менделеева
где:
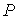 - давление газа, - давление газа, 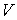 - занимаемый им объем, - занимаемый им объем, 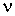 - количество молей идеального газа, - количество молей идеального газа, 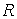 - универсальная газовая постоянная, - универсальная газовая постоянная, 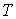 - абсолютная температура. Уравнение (2.2) названо в честь французского физика Поля Эмиля Клапейрона (1799 - 1864) и русского химика Дмитрия Ивановича Менделеева (1834 - 1907). - абсолютная температура. Уравнение (2.2) названо в честь французского физика Поля Эмиля Клапейрона (1799 - 1864) и русского химика Дмитрия Ивановича Менделеева (1834 - 1907).В рамках термодинамического подхода газ, уравнение состояния которого, связывающие параметры
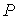 , , 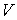 , и , и 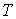 , является уравнением Клапейрона-Менделеева (2.2), называется идеальным газом. При нормальных условиях наиболее близкими по своим свойствам к идеальному газу являются водород и гелий. , является уравнением Клапейрона-Менделеева (2.2), называется идеальным газом. При нормальных условиях наиболее близкими по своим свойствам к идеальному газу являются водород и гелий.Подробный анализ уравнения (2.2) начнем с обсуждения величины
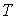 , которая называется абсолютной температурой. Из формулы (2.2) следует, что при постоянном объеме и количестве вещества температура , которая называется абсолютной температурой. Из формулы (2.2) следует, что при постоянном объеме и количестве вещества температура 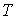 пропорциональна давлению идеального газа пропорциональна давлению идеального газа 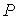 . А это означает, что если измерение температуры проводить с помощью газового термометра постоянного объема, в качестве рабочего тела в котором используется идеальный газ, то такой термометр будет иметь линейную шкалу температур. Очевидно, что использование газового термометра для определения абсолютной температуры ограничено, так как в качестве термометрического тела может быть использован только реальный газ, свойства которого отличны от идеального, и для которого уравнение (2.2) является приближенным, а при низких температурах не выполняется. . А это означает, что если измерение температуры проводить с помощью газового термометра постоянного объема, в качестве рабочего тела в котором используется идеальный газ, то такой термометр будет иметь линейную шкалу температур. Очевидно, что использование газового термометра для определения абсолютной температуры ограничено, так как в качестве термометрического тела может быть использован только реальный газ, свойства которого отличны от идеального, и для которого уравнение (2.2) является приближенным, а при низких температурах не выполняется.Абсолютная температура
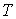 , измеренная с помощью рассмотренного идеально-газового термометра, связана с температурой, определенной по шкале Цельсия, выражением: , измеренная с помощью рассмотренного идеально-газового термометра, связана с температурой, определенной по шкале Цельсия, выражением:
где
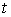 - численное значение температуры по шкале Цельсия. Единицей измерения температуры - численное значение температуры по шкале Цельсия. Единицей измерения температуры 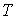 в абсолютной шкале температур является кельвин (К), численно совпадающий с единицей измерения температуры по шкале Цельсия - градусом Цельсия ((С). в абсолютной шкале температур является кельвин (К), численно совпадающий с единицей измерения температуры по шкале Цельсия - градусом Цельсия ((С).В соответствии с формулой (2.2) при абсолютной температуре
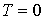 К произведение К произведение 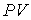 обращается в ноль. Это значение температуры называется абсолютным нулем температуры. Так же как и произведение давления на объем обращается в ноль. Это значение температуры называется абсолютным нулем температуры. Так же как и произведение давления на объем 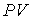 , абсолютная температура не может иметь отрицательных значений. Из (2.3) следует, что абсолютному нулю температуры соответствует , абсолютная температура не может иметь отрицательных значений. Из (2.3) следует, что абсолютному нулю температуры соответствует 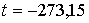 oC. oC.Перейдем к обсуждению введенного в формуле (2.2) параметра
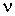 , который характеризует количество вещества, в данном случае идеального газа. С молекулярно-кинетической точки зрения, эта величина пропорциональна количеству молекул, входящих в систему. Очевидно, что от количества молекул в системе будут зависеть ее термодинамические свойства. Поэтому , который характеризует количество вещества, в данном случае идеального газа. С молекулярно-кинетической точки зрения, эта величина пропорциональна количеству молекул, входящих в систему. Очевидно, что от количества молекул в системе будут зависеть ее термодинамические свойства. Поэтому 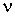 также как также как 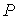 , , 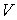 , и , и 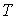 является термодинамическим параметром системы и уравнение состояния (2.2) связывает все эти четыре термодинамических параметра. Так как термодинамика не рассматривает молекулярную структуру вещества, то в ее рамках количество вещества может быть определено только из термодинамических соотношений на основе экспериментальных данных. является термодинамическим параметром системы и уравнение состояния (2.2) связывает все эти четыре термодинамических параметра. Так как термодинамика не рассматривает молекулярную структуру вещества, то в ее рамках количество вещества может быть определено только из термодинамических соотношений на основе экспериментальных данных.Проведенные опыты показали, что соотношение между параметрами
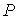 , , 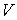 , и , и 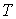 для разных газов остается одинаковым, если между их массами поддерживается определенное постоянное отношение. Например, коэффициент пропорциональности между произведением давления газа на его объем: для разных газов остается одинаковым, если между их массами поддерживается определенное постоянное отношение. Например, коэффициент пропорциональности между произведением давления газа на его объем: 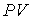 , и температурой , и температурой 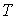 остается одинаковым как для 2 грамм водорода, так и для 32 грамм кислорода. Из этого следует (см. формулу (2.2)), что количество вещества остается одинаковым как для 2 грамм водорода, так и для 32 грамм кислорода. Из этого следует (см. формулу (2.2)), что количество вещества 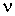 можно определить как отношение массы можно определить как отношение массы 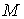 газа к некоторой постоянной для данного газа величине газа к некоторой постоянной для данного газа величине 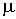 : :
где:
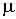 - называется молярной массой или массой одного моля вещества. - называется молярной массой или массой одного моля вещества.Понятие количества вещества исторически было сначала введено в химии для определения соотношения между массами вступающих в реакцию и получаемых в ней химических веществ. Это наложило отпечаток на определение единицы измерения количества вещества. Количество вещества измеряется в молях. Эта единица измерения внесена в список основных единиц системы СИ. Моль является безразмерной единицей и в принципе может быть опущен при записи.
Одним молем какого-либо вещества называется количество этого вещества, содержащее столько же молекул, сколько содержится в 12 граммах изотопа углерода
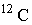 . .Количество молекул в одном моле любого вещества одинаково и численно равно постоянной Авогадро, названной в честь итальянского физика и химика Амедео Авогадро (1776 - 1856). Величина этой постоянной определялась экспериментально и численно равна:
Постоянная Авогадро показывает соотношение масштабов масс в макро- и микромире и является единицей измерения числа частиц в термодинамической системе. Она позволяет ввести критерий применимости термодинамического подхода при описании систем. Если число частиц в системе сравнимо или значительно превышает постоянную Авогадро, то для такой системы возможно термодинамическое описание.
Постоянная Авогадро связана с величиной, называемой атомной единицей массы (а.е.м.). Эта величина численно равна одной двенадцатой массы изотопа углерода
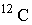 : :
Отношение одного грамма к атомной единице массы дает значение постоянной Авогадро.
Массу одного атома
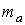 можно определить как произведение атомной единицы массы можно определить как произведение атомной единицы массы 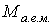 на атомную массу элемента на атомную массу элемента 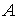 , указанную в таблице Менделеева: , указанную в таблице Менделеева:
Масса одной молекулы
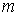 определяется как сумма масс атомов, входящих в неё. Умножение получившегося выражения на постоянную Авогадро дает молярную массу вещества: определяется как сумма масс атомов, входящих в неё. Умножение получившегося выражения на постоянную Авогадро дает молярную массу вещества:
Молярная масса измеряется в кг/моль.
В уравнении Клапейрона-Менделеева (2.2) в качестве коэффициента пропорциональности между величинами
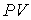 и и 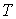 стоит произведение количества вещества стоит произведение количества вещества 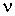 на коэффициент на коэффициент 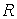 , который называется универсальной газовой постоянной. Эта величина одинаковая для всех газов: , который называется универсальной газовой постоянной. Эта величина одинаковая для всех газов:
Подстановка выражения для количества вещества (2.4) в уравнение Клапейрона-Менделеева (2.2) приводит его к окончательному виду
Уравнение Клапейрона-Менделеева описывает равновесные состояния идеального газа, а, следовательно, и любые обратимые процессы, которые в нем могут протекать. При наложении на систему дополнительных условий, можно получить уравнения термодинамических процессов, и соответствующие им законы, которые имеют ограниченное применение и являются частными случаями процесса, описываемого уравнением (2.10).
Согласно закону Бойля-Мариотта для неизменной массы газа при постоянной температуре давление газа меняется обратно пропорционально объёму, занимаемому газом. Процесс, описываемый этим законом, называется изотермическим (
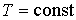 ), и его уравнение имеет вид: ), и его уравнение имеет вид:
Указанная связь между давлением и объёмом была независимо друг от друга изучена во второй половине ХVII века английским физиком Робертом Бойлем (1627 - 1691) и французским физиком Эдмом Мариоттом (1620 - 1684). В шестидесятых годах ХVII столетия Бойлем были проведены опыты по определению изменения объёма, занимаемого постоянным количеством воздуха, в зависимости от давления. Эти опыты носили чисто прикладной характер, связанный с разработкой и усовершенствованием Бойлем воздушных насосов. Для своих опытов Бойль использовал стеклянные трубки, запаянные с одного конца, в которые он заливал ртуть, оставляя около запаянного конца пузырёк воздуха. При измерениях для давления выше атмосферного использовалась изогнутая V-образная трубка, а в случае давления ниже атмосферного - прямая трубка, открытый конец которой помещался в сосуд с ртутью. По объёму пузырька и высоте столба ртути Бойль рассчитывал соотношение между давлением и объёмом воздуха. Полученные им данные подтвердили обратную зависимость между давлением и объёмом воздуха. В 1676 году закон Бойля был заново открыт Мариоттом, который рассматривал его как одно из фундаментальных свойств газов.
По мере развития методов измерения температуры стало возможным получение количественных соотношений между изменением объёма газов и их температурой. Жозар-Луи Гей-Люссак (1778 - 1850) провёл серию опытов для различных газов и установил, что при постоянном давлении и одинаковом количестве вещества расширение газов происходит одинаково при повышении температуры на одну и туже величину. Ранее, в конце ХVIII века, этот закон был установлен Жаком АлександромЦезарем Шарлем (1746 - 1823), но не был опубликован им.
Установленный ими закон описывает изобарический (
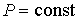 ) процесс: ) процесс:
или
где:
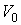 - объем газа при температуре равной нулю градусов по шкале Цельсия, - объем газа при температуре равной нулю градусов по шкале Цельсия, 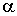 - температурный коэффициент расширения газа, который для идеального газа должен быть равен 1/273,15. Для реальных газов при нормальных условиях он близок к этому значению. - температурный коэффициент расширения газа, который для идеального газа должен быть равен 1/273,15. Для реальных газов при нормальных условиях он близок к этому значению.Если оставлять неизменным объем газа, что, например, имеет место в газовых термометрах постоянного объема, то происходящий при этом процесс будет называться изохорическим (
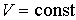 ) и описываться уравнением: ) и описываться уравнением:
Процессы в идеальном газе, происходящие при постоянстве одного из параметров состояния: температуры, давления или объема (см. уравнения (2.11), (2.12) и (2.14)), называются изопроцессами. Протекание этих процессов ограничено дополнительными внешними воздействиями, делающими один из параметров состояния постоянным. По этой причине эти процессы необходимо рассматривать только как частные случаи, которыми не ограничен перечень всех возможных обратимых процессов в идеальном газе.
|
|
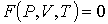 .
.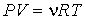 ,
,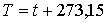 ,
,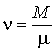 ,
,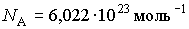 .
.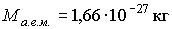 .
.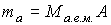 .
.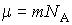 .
.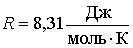 .
.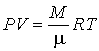 .
.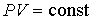 .
.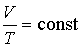 ,
,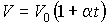 ,
,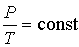 .
.